You will need
- calculator;
- - protractor;
- - the range.
Instruction
1
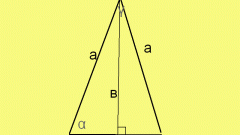
To find the area of a triangle, multiply the length of its side to the height (the perpendicular on this side from the opposite vertex) and divide the resulting product by two. As a formula this rule as follows:
S = ½ * a * h,
where:
S – the area of the triangle
a – the length of its sides,
h – the height lowered on this side.
The length of the side and height should be in the same units. The area of a triangle work in the appropriate "square" units.
S = ½ * a * h,
where:
S – the area of the triangle
a – the length of its sides,
h – the height lowered on this side.
The length of the side and height should be in the same units. The area of a triangle work in the appropriate "square" units.
2
Example.
One of the sides of scalene triangle with a length of 20 cm, dropped a perpendicular from the opposite vertex, length 10 cm
You want to determine the area of a triangle.
Solution.
S = ½ * 20 * 10 = 100 (cm2).
One of the sides of scalene triangle with a length of 20 cm, dropped a perpendicular from the opposite vertex, length 10 cm
You want to determine the area of a triangle.
Solution.
S = ½ * 20 * 10 = 100 (cm2).
3
If you know the lengths of any two sides of scalene triangle and the angle between them, then use the formula:
S = ½ * a * b * sinγ,
where: a, b – lengths of any two sides, and γ is the angle between them.
S = ½ * a * b * sinγ,
where: a, b – lengths of any two sides, and γ is the angle between them.
4
In practice, for example, when measuring the area of land, the use of the above formulas is sometimes difficult, as it requires additional constructs and measurement of angles.
If you know the lengths of all three sides of scalene triangle, use Heron's formula:
S = √(p(p-a)(p-b)(p-c)),
where:
a, b, c the lengths of the sides of the triangle
R – properiter: p = (a+b+c)/2.
If you know the lengths of all three sides of scalene triangle, use Heron's formula:
S = √(p(p-a)(p-b)(p-c)),
where:
a, b, c the lengths of the sides of the triangle
R – properiter: p = (a+b+c)/2.
5
If in addition the lengths of all sides known radius inscribed in a triangle circumference, use the following compact formula:
S = p * r,
where: r is the inradius (R – properiter).
S = p * r,
where: r is the inradius (R – properiter).
6
To compute the area of a versatile triangle via the radius of the circumscribed circle and the length of its sides, use the formula:
S = abc/4R,
where: R is the radius of the circumscribed circle.
S = abc/4R,
where: R is the radius of the circumscribed circle.
7
If we know the length of one side of a triangle and the values of the three angles (in principle, only two, the third value is calculated from the equality of the sum of the three angles of a triangle is 180º), then use the formula:
S = (a2 * sinβ * sinγ)/2sinα,
where α is the magnitude of the opposite side and corner;
β, γ are the values of the other two angles of the triangle.
S = (a2 * sinβ * sinγ)/2sinα,
where α is the magnitude of the opposite side and corner;
β, γ are the values of the other two angles of the triangle.