You will need
- Knowledge of geometry.
Instruction
1
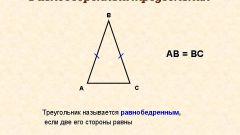
Let the given side of a right triangle with length a=7. Knowing this triangle can easily calculate its area. To do this, use the following formula: S = (3^(1/2)*a^2)/4. Substitute in this formula the value a=7 and obtain the following: S = (7*7*3^1/2)/4 = 49 * 1,7 / 4 = 20,82. Thus received that the area of an equilateral triangle with side a=7 is equal to S=20,82.
2
If given the radius of the inscribed triangle of a circle, the formula area using the radius will look like the following:
S = 3*3^(1/2)*r^2, where r is the radius of the inscribed circle. Let the radius of the inscribed circle r=4. Place it into the previously written formula and get the following expression: S = 3*1,7*4*4 = 81,6. That is, when the radius of the inscribed circle is 4 the area of an equilateral triangle will be equal to an 81.6.
S = 3*3^(1/2)*r^2, where r is the radius of the inscribed circle. Let the radius of the inscribed circle r=4. Place it into the previously written formula and get the following expression: S = 3*1,7*4*4 = 81,6. That is, when the radius of the inscribed circle is 4 the area of an equilateral triangle will be equal to an 81.6.
3
When you know the radius of the circumscribed circle formula area of a triangle is: S = 3*3^(1/2)*R^2/4, where R is the radius of the circumscribed circle. Suppose that R=5, substitute this value into the formula: S = 3*1,7*25/4 = 31,9. It turns out that when the radius of the circumscribed circle is equal to 5 the area of a triangle is equal to 31.9.
Note
The area of a triangle is always a positive value, as well as the length of a side of a triangle and the radii of the inscribed and circumscribed circles.
Useful advice
The radius of the inscribed and circumscribed circle in an equilateral triangle in two different times, knowing this, you can remember only one formula, for example, through the radius of the inscribed circle, and the second output, knowing this statement.