Instruction
1
Task one: calculate the volume, knowing the height and area. This is a simple task, because the area (S) is the product of length and width (S= l*(b), and the volume is the product of length, width and height. Substitute in the formula for volume is l*b area. You will get an expression V=S*h.Example: the Area of one side of the parallelepiped is 36 cm2, height 10 cm Find the volume of the parallelepiped.V = 36 cm2 x 10 cm = 360 cm3.Answer: the volume of the parallelepiped is equal to 360 cm3.
2
Task two: calculate volume knowing only area. This is possible if you calculate the volume of a cube knowing the area of one of its faces. Because the edges of the cube are equal, then removing from the value of the square of the square root, you get the length of one edge. This length will be the height and width.Example: the area of one face of a cube is 36 cm2. Calculate the volume.Extract the square root of 36 cm2. You've got a length of 6 cm For a cube the formula will be: V = a3, where a is the edge of the cube. Or V = S*a, where S is the area of one side, and the edge (height) of the cube.V = 36 cm 2 * 6 cm = 216 cm3. Or V = 63cm = 216 cm3.Answer: the Volume of a cube is 216 cm3.
3
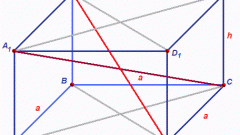
Task three: calculate volume if we know the area and some other conditions. Conditions can be different, in addition to the area may be aware of other options. Length or width can be equal to height, more or less than the height several times. May also be given additional information about the figures that will help in the volume calculations.Example 1: find the volume of the prism if you know the area of one side of 60 cm2, a length of 10 cm and a height equal to the width.S = l * b; l = S : b
l = 60 cm 2 : 10 cm = 6 cm width of the prism. Because the width and height, calculate the volume:
V=l*b*h
V = 10 cm * 6 cm *6 cm = 360 см3Ответ:the volume of the prism is 360 cm3
l = 60 cm 2 : 10 cm = 6 cm width of the prism. Because the width and height, calculate the volume:
V=l*b*h
V = 10 cm * 6 cm *6 cm = 360 см3Ответ:the volume of the prism is 360 cm3
4
Example 2: find the volume of the figure if the area of 28 cm2, the length of the figure 7, see Additional condition: four sides equal, and are connected to each other in width.For the solution you want to build a box. l = S : b
l = 28 cm2 7 cm = 4 cm – shiranakatta side is a rectangle whose length is 7 cm and width 4 cm If four such rectangle to interconnect width, we get a parallelepiped. The length and width in it at 7 cm and height 4 cm V = 7 cm * 7 cm * 4 cm = 196 см3Ответ: Volume of parallelepiped = 196 cm3.
l = 28 cm2 7 cm = 4 cm – shiranakatta side is a rectangle whose length is 7 cm and width 4 cm If four such rectangle to interconnect width, we get a parallelepiped. The length and width in it at 7 cm and height 4 cm V = 7 cm * 7 cm * 4 cm = 196 см3Ответ: Volume of parallelepiped = 196 cm3.