How to find the area and volume of a cube

The volume of a box is: V = abc, where a, b, c is its dimension. Therefore, the volume of a cube is equal to V = a*a*a = a^3, where a is the side length of the cube.The surface area of a cube is equal to the sum of the areas of all its faces. Only the cube has six faces, so the area of its surface equal to S = 6*(a^2).

Let the ball inscribed in the cube. Obviously, the diameter of the ball is equal to the side of the cube. Substituting the length of the diameter in the expression for the volume instead of the length of the edges of the cube and using that the diameter is twice the radius, then get V = d*d*d = 2r*2r*2r = 8*(r^3) where d is the diameter of the inscribed circle, and r is the radius of the inscribed circle.The surface area of the cube will then be equal to S = 6*(d^2) = 24*(r^2).

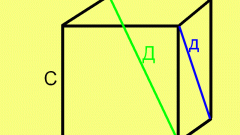
Let the ball circumscribed around the cube. Then its diameter will coincide with the diagonal of the cube. The diagonal of the cube passes through the center of the cube and connects two opposite points.
Consider first one of the faces of the cube. The edges of this face are the legs of a right triangle in which the face diagonal d is the hypotenuse. Then by the Pythagorean theorem we get: d = sqrt((a^2)+(a^2)) = sqrt(2)*a.

Then consider the triangle in which the hypotenuse is the diagonal of a cubeand the diagonal edge of d and one edge of cube a to his legs. Similarly, by the Pythagorean theorem we get: D = sqrt((d^2)+(a^2)) = sqrt(2*(a^2)+(a^2)) = a*sqrt(3).
So, derived the formula of diagonal of a cube is equal to D = a*sqrt(3). Hence, a = D/sqrt(3) = 2R/sqrt(3). Therefore, V = 8*(R^3)/(3*sqrt(3)), where R is the radius of the ball is described.The surface area of a cube is equal to S = 6*((D/sqrt(3))^2) = 6*(D^2)/3 = 2*(D^2) = 8*(R^2).