You will need
  • - handle;
  • paper for records;
  • calculator.
Instruction
1
The first method to find the height – using the area of a triangle. The area of a triangle is calculated by the formula: S = 1/2 ah, where (a) is a side of the triangle, h is the height, built to the side (a). From this expression, find the height: h = 2S/a.
2
If the condition given length of three sides of a triangle, find the area by Heron's formula: S = (p*(p-a)*(p-b)*(p-c))^1/2, where p is properietor of the triangle; a, b, C – sides. Knowing the area, you can determine the length of the altitude to any side.
3
For example, in the problem set, the perimeter of the triangle, which is inscribed in a circle with known radius. Calculate the area of the expression: S = r*p where r is the radius of the inscribed circle; p – pauperised. Of square, calculate the altitude to the side whose length you know.
4
The area of a triangle can also be determined by the formula: S = 1/2ab*sina, where a and b are the sides of a triangle; sina is the sine of the angle between them.
5
Another case – you know all the angles of a triangle and one side. Use the theorem of sines: a/sina = b/sinb = C/sinc = 2R, where a, b, c be the sidelengths of triangle; sina, sinb, sinc sines of the angles opposite to these sides; R is the radius of the circle which is described around the triangle. Find the direction of b from the relationship: a/sina = b/sinb. Then calculate the area of the same way as in step 4.
6
The second way to calculate the height is to use the trigonometric relationships for a right triangle. The height of the acute-angled triangle divides it into two rectangular. If we know the side opposite the base (a), and the angle between them, use the expression: h = b*sina. In obtuse-angled triangle, because the angle (a) blunt, the formula is slightly different: h = b*sin(180-a) or h = - c*sina.
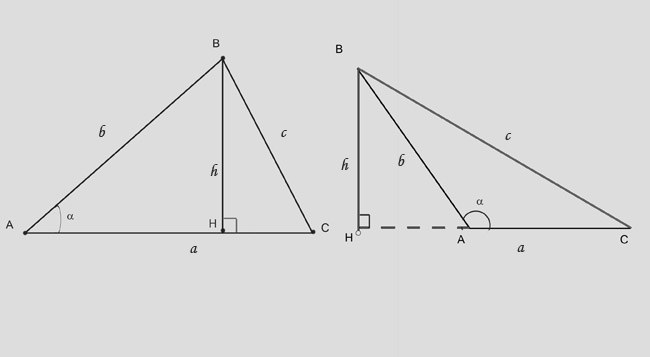
How to determine the height of the triangle
7
If you are given the height opposite the angle and the length of the segment AH which cuts off the height from the base, use the equation: BH = (AH)*the tga.
8
Also, knowing the length of the segment AH, and the sides AB, find the height HV of the Pythagorean theorem: BH = (AB^2 – BC^2)^1/2.