How to inscribe a circle in a rhombus

Draw a rhombus with the given parameters. You must know the length of the side and at least one corner. This can be done in an ordinary school notebook in the box and on the computer. For a rough figure, intended for instance for the presentation, I will even take the Word with the drawing function. But in this program, you will be able to submit only a General view, without calculations. So draw in AutoCAD, or on a sheet of paper checked for many centuries way. In the first case find in the menu the function "Polygon". Choose build over the length of the hand and its position. Enter the number of sides and angle.

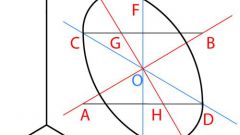
When you build a diamond pattern on a sheet of paper, draw a horizontal line, the length of which corresponds to a given size of hand. Using the protractor set aside from it a specified angle and poluchivshimsya ray put the same size. Two other sides of the guide parallel to the existing one. Mark diamond as АBCD.

Remember the properties of a rhombus and the inscribed circle. In any quadrilateral that can be inscribed circle, whose center lies at the intersection of the bisectors. In the rhombus are bisectors of the angles both diagonals. That is, in order to find the center of the circle, you need to spend. Mark the center of the circle as O.

Inscribed circle touches all sides of the polygon. That is, the sides of the rhombus will be both tangent. Remember the tangent lines. It is perpendicular to the radius, held in the touch point. It is necessary to spend from the center of the circle perpendicular to at least one of its sides. Put a point N.

Put the needle of a compass to the point About, and stretch his legs at a distance ON. Draw a circle. It will have touch points with all sides of a rhombus.

If you want to calculate the radius of the inscribed circle, do it by applying different formula of the area of the figure. S=a*h, where a is specified in the condition side, and h is the height. The height of the rhombus is both twice the radius of the inscribed circle, that is the formula of square can be represented as S=2ar. At the same time, S=a2*sinα. It turns out that 2ar=a2*sinα. Find the unknown value of r. Radius equal to the quotient from division of product of square sides and the sine of an angle twice the direction. That is, r=a2*sinα/2a.

Inscribed circle in the Autocad program build on the already known center and radius was found. To do this in the main menu, locate the toolbar "Drawing". Find the drop down window "Circle" and select "center, radius". Center: specify with the cursor.