Instruction
1
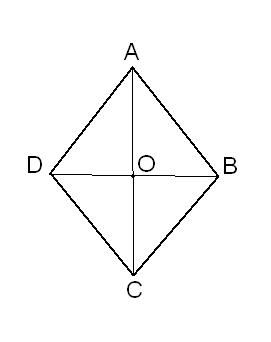
The perimeter of a rhombus can be calculated, knowing the length of its side. In this case, by definition the perimeter of a rhombus is equal to the sum of the lengths of its sides, and therefore equal to 4a, where a is the side length of the rhombus.
2
If you know the area of a rhombus and the ratio between the diagonals, the problem of finding the perimeter of a rhombus is slightly more complicated. Given the area of a rhombus S and the ratio of the diagonals AC/BD = k. Area of a rhombus can be expressed through the product of the diagonals: S = AC*BD/2. Triangle AOB is a right triangle because the diagonals of a rhombus intersect at a 90° angle. Side of the rhombus AB by theorem of Pythagoras can be found from the following expression: AB2 = AO2 + OB2. Since the rhombus is a special case of a parallelogram and in a parallelogram the diagonals bisect the point of intersection, then AO = AC/2 and OB = BD/2. Then AB2 = (AC2 + BD2)/4. The condition AC = k*BD, then 4*AB2 = (1 + k2)*BD2.
Express BD2 through the area:
S = k*BD*BD/2 = k*BD2/2
BD2 = 2*S/k
Then 4*AB2 = (1 + k2)*2S/k. Hence AB is equal to the square root of S(1 + k2)/2k. And the perimeter of a rhombus is still equal to 4*AB.
Express BD2 through the area:
S = k*BD*BD/2 = k*BD2/2
BD2 = 2*S/k
Then 4*AB2 = (1 + k2)*2S/k. Hence AB is equal to the square root of S(1 + k2)/2k. And the perimeter of a rhombus is still equal to 4*AB.