Instruction
1
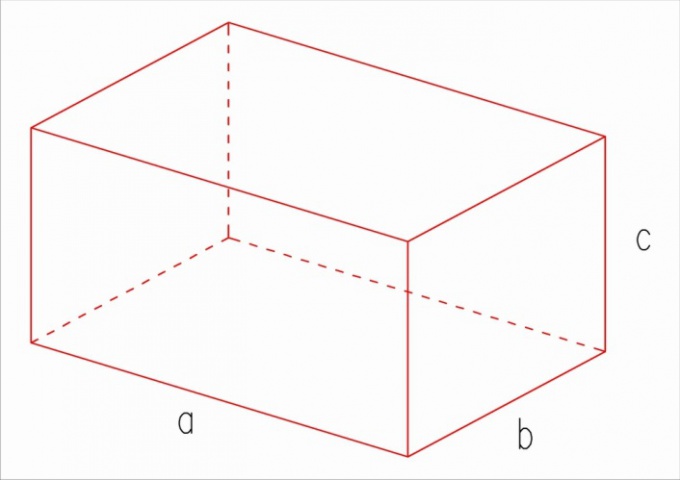
To begin calculate the area of three different faces of the parallelepiped. For example, the length of the box (a) is 7 cm, width (b) 6 cm, and the height (C) 4 cm Then the area of the upper (lower) faces will be equal to ab, i.e. 7x6=42 cm Area of one of the side faces will be equal to bc, i.e., 6x4=24, see Finally, the area of the front (rear) face is equal to ac, i.e. 7 × 4=28 cm.
2
Now let's add up all three scores and multiply the resulting sum by two. In our it will look like the following: 42+24+28=94; 94х2=188. Thus, the surface area of this cuboid is equal to 188 cm
Note
Be careful not to confuse a rectangular parallelepiped with direct. The direct parallelepiped rectangles are only the side faces (4 of the 6 faces), and the upper and lower bases are arbitrary parallelograms.
Useful advice
As a particular case of a rectangular parallelepiped can be considered CC, since all its faces are equal, then for finding the surface will be necessary to erect the edge length in the square and multiply by 6.