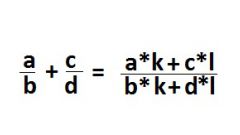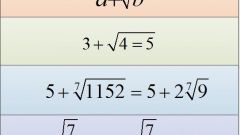Instruction
1
Suppose that you want to compare two irrational numbers. The first thing you should pay attention to is the exponents of the roots of the numbers being compared. If the indicators are the same, compare radical expression. Obviously, the more radical the number, the greater the value of the root at equal rates. For example, suppose you need to compare the cube root of two and the cube root of eight. The indicators are the same and equal to 3, radical expressions 2 and 8 and 2 < 8. Consequently, the cube root of two less than the cube root of eight.
2
In another case, the exponents can be different, and radical expressions are the same. Also it is clear that the root more get fewer.Take for example the cube root of eight and the root of the sixth power of eight. If we denote the value of the first root as a and second as b, then a^3 = 8 and b^6 = 8. It is easy to see that a must be greater than b, so the cube root of eight more of the root of the sixth power of eight.
3
More complicated is the situation with different exponents roots and radical expressions different. In this case, it is necessary to find the least common multiple of the indices of the roots and build both expressions in a degree equal to the least common multiple.Example: need to compare 3^1/3 and 2^1/2 (mathematical notation has roots in the figure). Least common multiple for 2 and 3 is 6. Lift both the root of the sixth degree. There also turns out that 3^2 = 9 and 2^3 = 8, 9 > 8. Consequently, 3^1/3 > 2^1/2.
Useful advice
To compare arithmetic expressions composed of several roots, have lead to a common root. This can be done by using formulas of abridged multiplication formula of the Binomial theorem and other techniques.