You will need
  • Program for drawing, pencil, paper, eraser, protractor.
Instruction
1
A rectangular projection. Isometric projection. When you build a rectangular isometric projection take into account the distortion ratio in the X, Y, Z, equal to 0.82, while the circumference parallel to the planes of projection are projected on the axonometric plane of projections in the form of ellipses, the major axis of which is equal to d and with a minor axis of 0.58 d, where d is the diameter of the original circle. For ease of calculation isometric projection are performed without distortion of the axes (distortion factor equal to 1). In this case, the projected circle will have the form of ellipses with the major axis, equal to 1.22 d, and the minor axis equal to d of 0.71.
2
Dieticheskaya projection. When building rectangular dimetrically projection takes into account the distortion factor along the axes X and Z, equal to 0.94, and the Y – axis is 0.47. In practice dieticheskoe projection simplistically perform without distortion in X and Z and the distortion factor along the Y-axis = 0,5. A circle parallel to the frontal plane of projection is projected onto her in the form of an ellipse with the major axis equal to 1.06 d and the minor axis, is equal to 0,95 d, where d is the diameter of the original circle. Circle, parallel to the other two axonometric planes are projected onto them in the form of ellipses with the axes, respectively, equal to 1.06 d and 0.35 d.
The construction of the axonometric projection. Figure 3
3
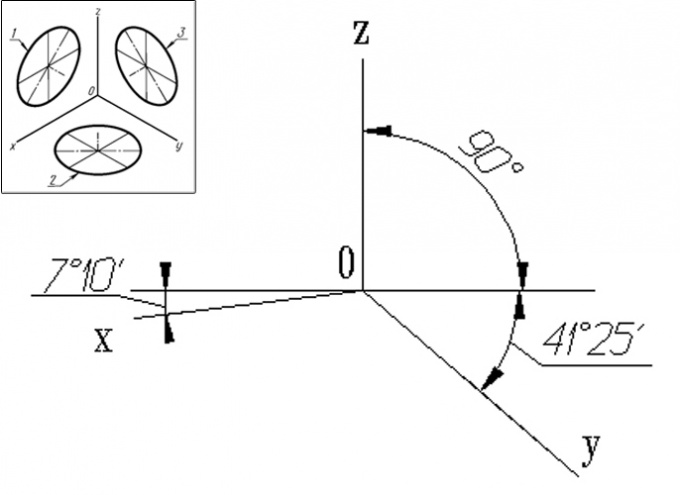
Oblique projection. Frontal isometric projection. When building a front isometric view standard the optimum angle of the axis Y to the horizontal of 45 degrees. Allowed tilt angles of the Y-axis to the horizontal - 30 degrees and 60 degrees. The distortion ratio in the X, Y, and Z equal to 1. Circumference 1, located parallel to the frontal plane of projection is projected onto it without distortion. Circles parallel to the horizontal and profile planes of projections, made in the form of ellipses 2 and 3 with the major axis equal to 1.3 d and a minor axis equal to 0,54 d, where d is the diameter of the original circle.
The construction of the axonometric projection. Figure 4
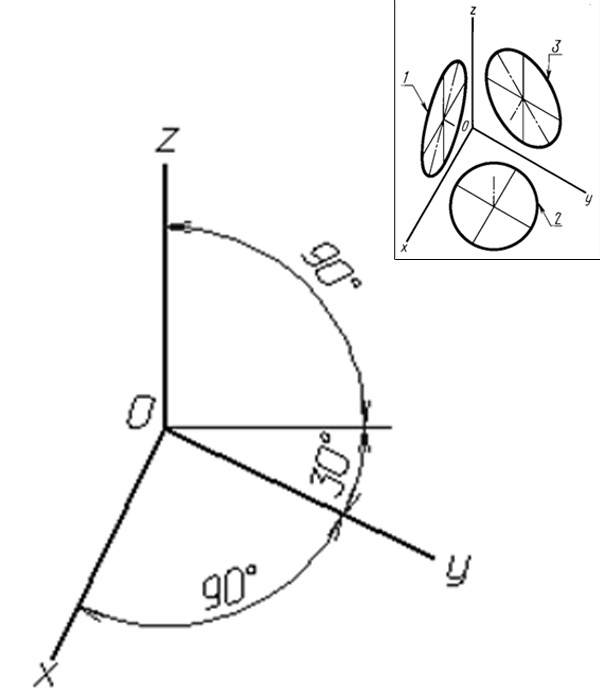
4
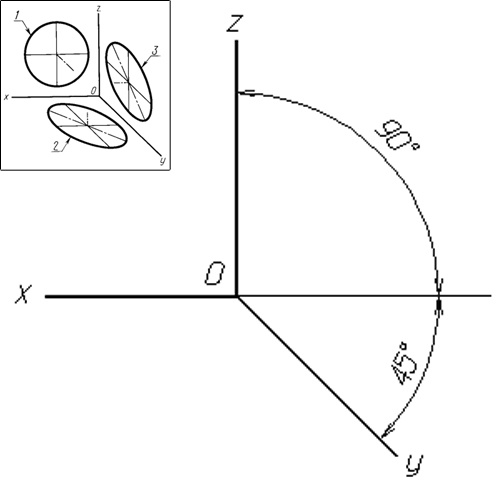
Horizontal isometric projection. Horizontal isometric projection of the part (node) is based on the axonometric axes are located as shown in Fig. 7. You can change the angle between the Y axis and the horizontal is 45 degrees and 60 degrees, to keep the same 90 degree angle between axes Y and X. the distortion Ratio in the X, Y, Z equal to 1. A circle lying in a plane parallel to the horizontal plane of projection is projected in the form of a circle 2 without distortion. Circle, parallel, frontal and profile planes of projections have the form of ellipses 1 and 3. The dimensions of the axes of the ellipses associated with the initial diameter d of a circle the following relationship:
1 ellipse – major axis equal to 1.37 d, the minor axis is 0, 37d; 3 ellipse – major axis equal to 1.22 d, the minor axis – 0.71 d.
The construction of the axonometric projection. Figure 5
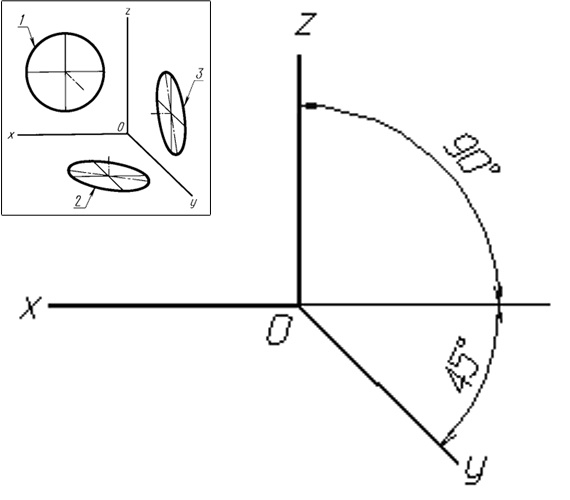
5
Dieticheskaya front projection. Dieticheskaya oblique frontal projection of the part (node) is based on the axonometric axes similar to the axes of the frontal isometric projection, but differ from it the distortion factor along the Y-axis, which is equal to 0.5. The X-and Z-distortion factor equal to 1. It is also possible to change the angle of the Y-axis to the horizontal up to 30 degrees and 60 degrees. A circle lying in a plane parallel to a frontal axonometric plane of projections), is projected to it without distortion. The circumference parallel to the planes of projection horizontal and profile, are plotted in the form of ellipses 2 and 3. The sizes of the ellipses of the size of the circle diameter d are expressed by the relationship:
the major axis of ellipses 2 and 3 is equal to 1.07 d; minor axis of ellipses 2 and 3 is equal to 0.33 d.
The construction of the axonometric projection. Figure 6