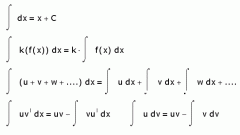How to investigate for convergence the series

By definition a series is called convergent, if there is a finite number, which obviously is more than the sum of the elements of this series. In other words, the series converges if the sum of its elements is finite. To reveal the fact, is the sum of a finite or infinite will help convergence tests for series.

One of the easiest signs of convergence is a sign of convergence Leibniz. We can use, if the series is alternating (that is, each successive member of the series changes the sign from "plus" to "minus"). On the basis of Leibniz alternating series is convergent if the last member of a number modulo tends to zero. For this purpose, the limit of the function f(n) flock n to infinity. If this limit is zero, then the series converges, otherwise diverges.

Another common way to check the number on the convergence .the convergence - limiting characteristic of d'alembert. To use it, we divide the n-th term of the sequence to the previous ((n-1)-yy). This relationship we computed, its result is taken modulo (n again to aspire to infinity). If we get a number less than unity, the series converges, otherwise the series diverges.

Radical sign d'alembert is somewhat similar to the previous one: we extract the root of n-th degree of the n-th member. If we get a number less than unity, then the sequence converges, sum of its members is a finite number.

In some cases (when we cannot apply the sign of d'alembert) advantageous to use the integral sign by Cauchy. For this a recorded function series under the integral, differential take n between the limits from zero to innity (this integral is called improper). If the numerical value of this improper integral equals a finite number, the series is convergent.

Sometimes in order to find out what type of a number, not necessarily to use the convergence tests. You can just compare it with another convergent series. If the number is less than obviously convergent series, then it is also convergent.