Instruction
1
Write down the given matrix. Determine the dimensionality. To do this, count the number of columns n and rows m. If for one matrix m = n, the matrix is considered to be square. If all the elements of the matrix equal to the zero matrix is zero. Define the main diagonal of the matrices. The switching elements are arranged from the upper left corner of the matrix to the bottom right. Second, the inverse of a diagonal matrix is a by.

2
Spend the transposition of a matrix. To do this, replace each matrix row elements on the column elements relative to the main diagonal. The element A21 will be the element A12 in the matrix and Vice versa. At the end of each of the source matrix get a new transposed matrix.
3
Fold the given matricesif they have the same dimension m x n. To do this, take the first element of the matrix A11 and fold it to the corresponding element b11 of the second matrix. The result of adding record in a new matrix at the same position. Then fold the elements A12 and b12 of both matrices. Thus complete all rows and columns summing matrix.
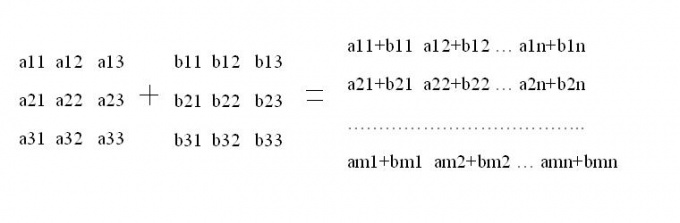
4
Determine whether the given matrix is consistent. To do this, compare the number of rows n in the first matrix and the number of columns m of the second matrix. If they are equal, perform the product of matrices. For this pairwise multiply each element of the row of the first matrix to the corresponding element in the column of the second matrix. Then find the sum of these products. Thus, the first element of the resulting matrix g11 = A11* b11 + A12*b21 + A13*b31 + ... + а1м*bn1. Perform the multiplication and addition of all works and fill in the result matrix G.
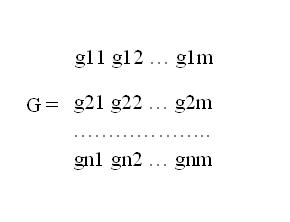
5
Find the determinant or determinants for any given matrix. For matrices of the second order - dimension 2 by 2 determinant is the difference of products of elements of main and secondary diagonals of the matrix. For the three-dimensional matrix formula of the determinant: D = A11* A22*A33 + A13* A21*A32 + A12* A23*A31 - A21* A12*A33 - A13* A22*A31 - A11* A32*A23.

6
To find the minor of a particular element of the zero matrix the row and column where is located this item. Then define the determinant of the obtained matrix. This will be a minor element.






