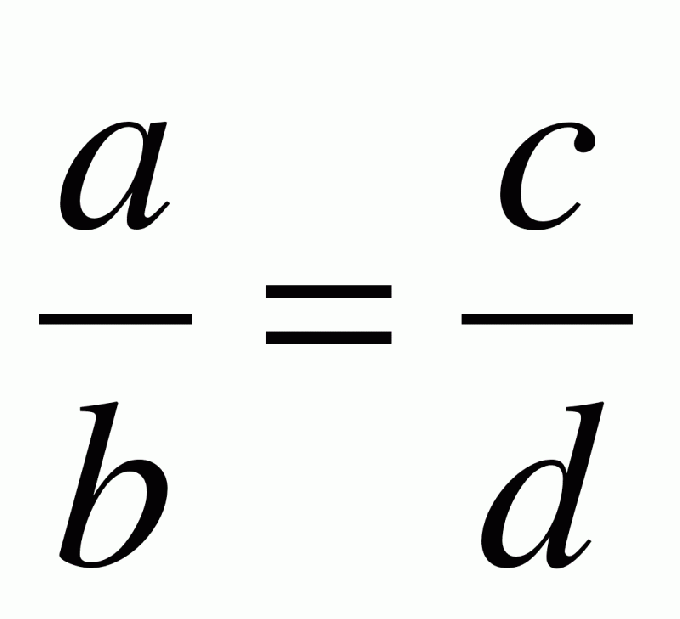How to find proportion

Inspect the properties of proportions. The numbers on the edges of the equality is called extreme, and in the middle – average. The main property of proportions is that the middle and the extreme side of the equation can be multiplied among themselves. Enough to take the proportion 8:4=6:3. If you multiply the extreme parts together, you get 8*3=24 and the multiplication of the averages. This means that the product of the extreme parts of the ratio is always equal to the product of its average parts.

Take advantage of the fundamental property of proportions to calculate the unknown member in the equation for x:4=8:2. For finding the unknown parts of a proportion you must use the rule of equivalence of average and extreme parts. Write the equation in the form x*2=4*8, that is x*2=32. Solve this equation (32/2), you will receive the missing member of the proportion (16).

Simplify the ratio if it consists of fractional or large numbers. To do this, divide or multiply both members on the same number. For example, the component parts of a 80:20 proportion=120:30 can be simplified, dividing its members into 10 (8:2=12:3). You will get an equivalent equality. The same thing happens if you increase all members of the proportion, for example, 2, thus 160:40=240:60.

Try to move your parts of proportions. For example, 6:10=24:40. Swap the extreme end (40:10=24:6), or at the same time rearrange all the parts (40:24=10:6). All received proportions are equal. So you can get some equations from one.

Solve the proportion with interest. Make a note of it, for example, in the form: 25=100%, 5=x. Now we need to multiply the average members (5*100) and divide by the known extreme (25). In the end, it turns out that x=20%. Similarly, you can multiply the known extreme members and to divide them into existing medium, receiving the desired result.