You will need
- pencil;
- - the range.
Instruction
1
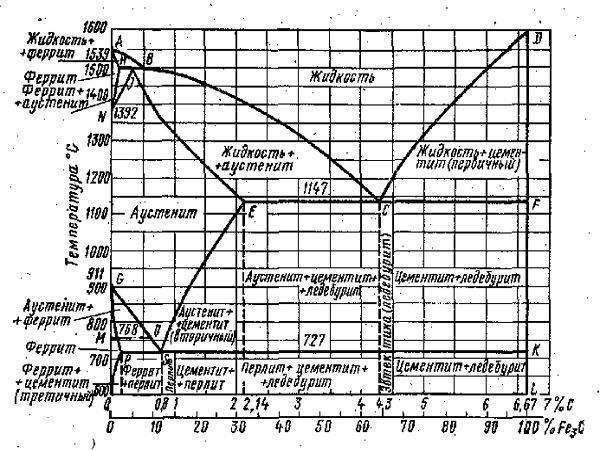
For example, you need to build the curve of cooling for the iron-carbon alloy. To start, determine what phases exist in the system. Thus, the alloys of iron and carbon phases represent austenite, ferrite, cementite and graphite.
2
Describe each of these phases. Ferrite is a structural component of an α-iron, which dissolves the carbon. Austenite – solid solution, which was the way of introduction in γ-iron is carbon. When the temperature of the austenite cementite is highlighted. Graphite is carbon, which is released in a free state in iron-carbon alloys.
3
To construct the curve of cooling use the Gibbs phase rule, which is formulated as follows: in the equilibrium system, which is influenced by only temperature and pressure, the number of degrees of freedom equals the difference in the number of components and number of phases is increased by 2.
4
The Gibbs phase rule is expressed by the formula: f = n - K + 2, where f is the number of degrees of freedom; n – number of components; K is the number of phases. Apply phase rule to the iron-carbon alloy, which has 2 components: the iron and carbon. Thus, point 1: f = 2 – 2 + 1 = 1 is the liquidus. The result indicates that the system is single-variant, i.e. changing the temperature of the alloy will remain in the same state of aggregation.
5
Calculate point 2 and 3: f = 2 – 3 + 1 = 0 is the solidus or eutectic transformation. The result indicates that the system is mandatory and any change will change the number of phases.
6
Making calculations, draw the curve of cooling. Draw a graph of temperature over time and indicate on it the main point. Connect the dots between them, you get a line a liquidus line and a solidus on the chart.
Note
In order to account for phase diagrams, it is necessary to know the structural components of the cooling curve which you build, and their properties depending on temperature change.
Useful advice
In some charts do not use time and other parameters, for example, the correlation between the temperature and thermal expansion.



