You will need
- Knowledge of the lengths of the sides of the triangle.
Instruction
1
To calculate the length of the median formula is applied (see Fig. 1), where:
mc is the length of the median;
a, b, c be the sidelengths of a triangle.
mc is the length of the median;
a, b, c be the sidelengths of a triangle.
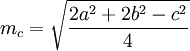
Note
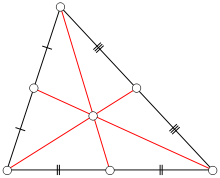
The medians of a triangle have the following properties:
1) any of the three medians divides the original triangle into two equal size triangle;
2) All medians of a triangle have a common intersection point. This point is called the center of the triangle;
3) the Medians of a triangle divide it into 6 equal triangles. Equal are called geometric shapes with equal areas.
1) any of the three medians divides the original triangle into two equal size triangle;
2) All medians of a triangle have a common intersection point. This point is called the center of the triangle;
3) the Medians of a triangle divide it into 6 equal triangles. Equal are called geometric shapes with equal areas.
Useful advice
If the triangle is an isosceles triangle, its medians are equal. In addition, in such a triangle the medians coincide with the bisectors and heights.
The angle bisector is the ray that emanates from any vertex of a triangle and forming it divides the angle in half.
Under the height of a triangle is meant the segment, which is drawn from the vertex of the triangle perpendicular to the opposite side.
The angle bisector is the ray that emanates from any vertex of a triangle and forming it divides the angle in half.
Under the height of a triangle is meant the segment, which is drawn from the vertex of the triangle perpendicular to the opposite side.