Instruction
1
Task 1.
In an arbitrary triangle ABD held the median BE. Find its length if it is known that the parties, respectively, equal to AB = 10 cm, BD = 5 cm and AD = 8 cm.
In an arbitrary triangle ABD held the median BE. Find its length if it is known that the parties, respectively, equal to AB = 10 cm, BD = 5 cm and AD = 8 cm.
2
Solution.
Apply the formula median expression across all sides of the triangle. This is a simple task, since all the lengths of the sides are known:
BE = √((2*AB^2 + 2*BD^2 - AD^2)/4) = √((200 + 50 - 64)/4) = √(46,5) ≈ 6,8 (cm).
Apply the formula median expression across all sides of the triangle. This is a simple task, since all the lengths of the sides are known:
BE = √((2*AB^2 + 2*BD^2 - AD^2)/4) = √((200 + 50 - 64)/4) = √(46,5) ≈ 6,8 (cm).
3
Task 2.
In the isosceles triangle ABD, the sides AD and BD are equal. Held the median from vertex D to the side of the BA, it is BA with the angle equal to 90°. Find the length of the median DH, if you know that BA = 10 cm, and the angle DBA equal to 60°.
In the isosceles triangle ABD, the sides AD and BD are equal. Held the median from vertex D to the side of the BA, it is BA with the angle equal to 90°. Find the length of the median DH, if you know that BA = 10 cm, and the angle DBA equal to 60°.
4
Solution.
To find the median, identify one and equal sides of the triangle AD or BD. For this we consider one of the right triangles, suppose BDH. From the definition of the median, it follows that BH = BA/2 = 10/2 = 5.
Find the side BD in the formula of the trigonometric properties of a right triangle - BD = BH/sin(DBH) = 5/sin60° = 5/(√3/2) ≈ 5,8.
To find the median, identify one and equal sides of the triangle AD or BD. For this we consider one of the right triangles, suppose BDH. From the definition of the median, it follows that BH = BA/2 = 10/2 = 5.
Find the side BD in the formula of the trigonometric properties of a right triangle - BD = BH/sin(DBH) = 5/sin60° = 5/(√3/2) ≈ 5,8.
5
Now there are two options for finding the median: the formula used in the first task or the Pythagorean theorem for a right triangle BDH: DH^2 = BD^2 - BH^2.
DH^2 = (5,8)^2 - 25 ≈ 8,6 (cm).
DH^2 = (5,8)^2 - 25 ≈ 8,6 (cm).
6
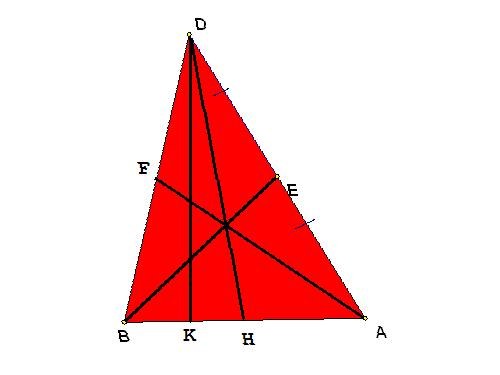
Task 3.
In an arbitrary triangle BDA carried out the three medians. Find the length if it is known that the height of the DK equal to 4 cm and divides the base into segments of length BK = 3 and KA = 6.
In an arbitrary triangle BDA carried out the three medians. Find the length if it is known that the height of the DK equal to 4 cm and divides the base into segments of length BK = 3 and KA = 6.
7
Solution.
To find the median of the necessary lengths of all sides. The length of the BA can be found from the conditions: BA = BH + HA = 3 + 6 = 9.
Consider a right triangle BDK. By the Pythagorean theorem find the length of the hypotenuse BD:
BD^2 = BK^2 + DK^2; BD = √(9 + 16) = √25 = 5.
To find the median of the necessary lengths of all sides. The length of the BA can be found from the conditions: BA = BH + HA = 3 + 6 = 9.
Consider a right triangle BDK. By the Pythagorean theorem find the length of the hypotenuse BD:
BD^2 = BK^2 + DK^2; BD = √(9 + 16) = √25 = 5.
8
Similarly, find the hypotenuse of a right triangle KDA:
AD^2 = DK^2 + KA^2; AD = √(16 + 36) = √52 ≈ 7,2.
AD^2 = DK^2 + KA^2; AD = √(16 + 36) = √52 ≈ 7,2.
9
According to the formula expressions using side find the median:
BE^2 = (2*BD^2 + 2*BA^2 - AD^2)/4 = (50 + 162 - 51,8)/4 ≈ 40, hence BE ≈ 6,3 (cm).
DH^2 = (2*BD^2 + 2*AD^2 - BA^2)/4 = (50 + 103,7 - 81)/4 ≈ 18,2, hence DH ≈ 4,3 (cm).
AF^2 = (2*AD^2 + 2*BA^2 - BD^2)/4 = (103,7 + 162 - 25)/4 ≈ 60, hence AF ≈ 7,8 (cm).
BE^2 = (2*BD^2 + 2*BA^2 - AD^2)/4 = (50 + 162 - 51,8)/4 ≈ 40, hence BE ≈ 6,3 (cm).
DH^2 = (2*BD^2 + 2*AD^2 - BA^2)/4 = (50 + 103,7 - 81)/4 ≈ 18,2, hence DH ≈ 4,3 (cm).
AF^2 = (2*AD^2 + 2*BA^2 - BD^2)/4 = (103,7 + 162 - 25)/4 ≈ 60, hence AF ≈ 7,8 (cm).