Instruction
1
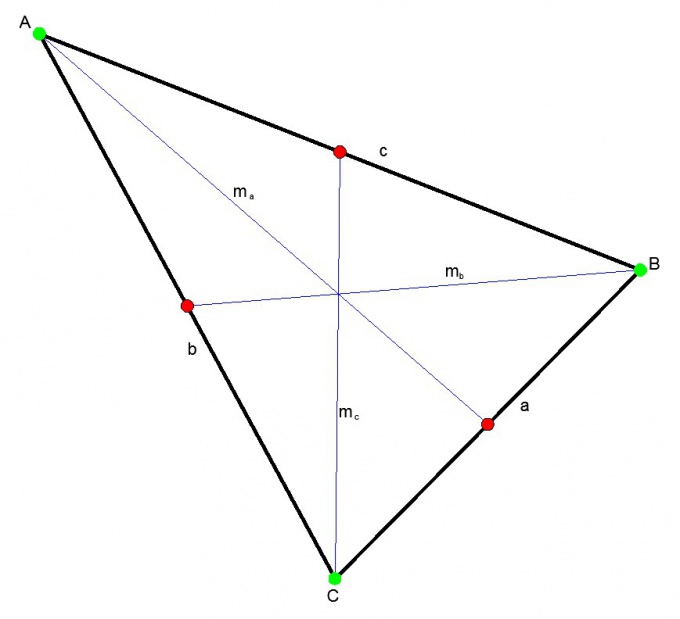
The median can be found using the theorem of Stewart. According to which, the square of the median is equal to a quarter of the amount of the matching squares of the sides minus the square of the side, which held the median.
mc^2 = (2a^2 + 2b^2 - c^2)/4,
where
a, b, c are sides of a triangle.
mc is the median to side C;
mc^2 = (2a^2 + 2b^2 - c^2)/4,
where
a, b, c are sides of a triangle.
mc is the median to side C;
2
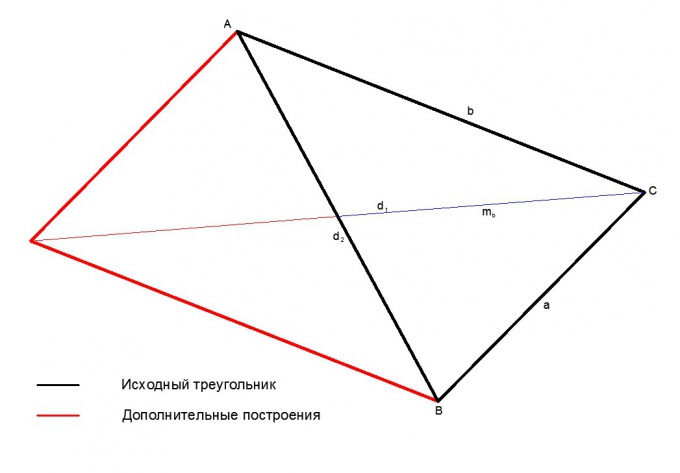
The task of finding the median can be solved using additional constructions of the triangle to the parallelogram and the solution using the theorem of the diagonals of a parallelogram.Extend the sides of a triangle and the median, to complete them to the parallelogram. Thus, median of a triangle is equal to half the diagonal of the resulting parallelogram, two sides of the triangle - its sides (a, b), and the third side of the triangle, which was a median, is the second diagonal of the resulting parallelogram. According to the theorem, the sum of the squares of the diagonals of a parallelogram is twice the sum of the squares of its sides.
2*(a^2 + b^2) = d1^2 + d2^2,
where
d1, d2 - diagonal of the resulting parallelogram;
from here:
d1 = 0.5*v(2*(a^2 + b^2) - d2^2)
2*(a^2 + b^2) = d1^2 + d2^2,
where
d1, d2 - diagonal of the resulting parallelogram;
from here:
d1 = 0.5*v(2*(a^2 + b^2) - d2^2)