Instruction
1
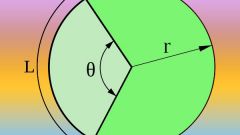
The circle sector is the portion of the figure bounded by two radii and an arc between the points of intersection of these radii with the circumference. Depending on the specified in the task parameters area of the sector can be expressed through the radius of the circle or arc length.
2
Area of full circle S through a circle radius r is determined by the formula:
S = π*r2
where π is a constant number equal 3,14.
Swipe in circle diameter, and the figure is divided into two halves each with an area s =S/2. Divide the circumference into four equal sections by two mutually perpendicular diameters, the area of each sector will be s = S/4.
Half of the circle represents the sector with the unfolded angle and the Central angle of the quarter circle is equal to a quarter of the full angle. Therefore, the area of an arbitrary sector, in many times smaller than the area of circle how many times the Central angle of this sector α is less than 360 degrees. Therefore the formula of area of sector of a circle can be written as S₁ = πr2*α/360.
S = π*r2
where π is a constant number equal 3,14.
Swipe in circle diameter, and the figure is divided into two halves each with an area s =S/2. Divide the circumference into four equal sections by two mutually perpendicular diameters, the area of each sector will be s = S/4.
Half of the circle represents the sector with the unfolded angle and the Central angle of the quarter circle is equal to a quarter of the full angle. Therefore, the area of an arbitrary sector, in many times smaller than the area of circle how many times the Central angle of this sector α is less than 360 degrees. Therefore the formula of area of sector of a circle can be written as S₁ = πr2*α/360.
3
Area of sector of a circle can be expressed not only through its Central angle but also through the arc length L of the sector. Draw a circle and spend two of arbitrary radius. Connect the points of intersection of the radii with the circumference of the line segment (chord). Consider the triangle formed by two radii and a chord, drawn through their ends. The area of this triangle is equal to half of the work of chord length to the height, drawn from the center of the circle to this chord.
4
If the height of the isosceles triangle is considered to extend to the intersection with the circumference, and the received point to connect with the ends of the radii, you will get two equal triangles. The area of each equal to half of the work base — chord to the height, drawn from the centre to the base. And the area of the original triangle is equal to the sum of the squares of two new figures.
5
If we continue the division of triangles, the height with each subsequent division will increasingly seek to radius of the circle, and that common factor in the expression area of the triangle as the sum of the squares can be put outside the brackets. Then in brackets will be the sum of the bases of the triangles, tending to the arc length of the initial sector of a circle. Then the formula of area of sector of a circle will take the form S = L*r/2.