How to find the area of an octagon

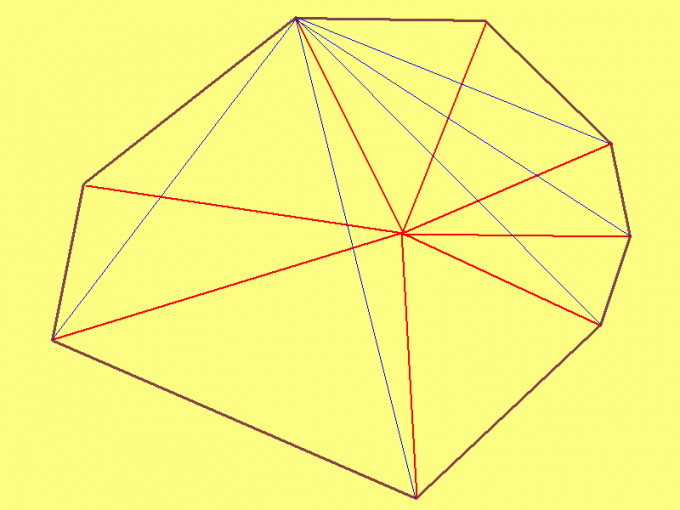
To find the area of an arbitrary octagon, click within arbitrary point and swipe from her segments to each vertex. Then measure the lengths of the sides of each of the eight resulting triangles. Then, using the Heron formula, calculate the area of each triangle. And finally, add the area of all triangles. The resulting amount will be the area of the octagon.

To use the Heron formula, calculate first properiter triangle:p = (a + b + c) / 2 where a, b, c the lengths of the sides of the triangle; p – marking of properiety.Considering properiter triangle, substitute the value obtained into the formula:S = √(p*(p-a)*(p-b)*(p-c)), where S is the area of a triangle.

If the octagon convex (no interior angles 180º large), the interior-point select any of the vertices of the octagon. In this case, you get a total of six triangles, which is a bit easier finding the area of an octagon. The method of calculation of areas of triangles is the same as described in the previous paragraph.

If an octagon has equal sides and angles, then this is the right geometrical shape – the octagon. To calculate the area of this octagon , use the formula:S = 2 * k * a2, where a is the length of sides of a regular octagon; k – coefficient equal to (1+√2)≈2,4142135623731.

In the solution of school problems sometimes is given the length of sides of a regular octagon, and the length of its largest and smallest diagonals. In this case, use the formula:S = d * D, where d is the length of the smaller diagonal; D is the length of the major diagonal.Larger diagonal of the octagon is a segment that connects two opposite vertices. Lower right diagonal of the octagon bude segment connecting the two vertices through one.