Instruction
1
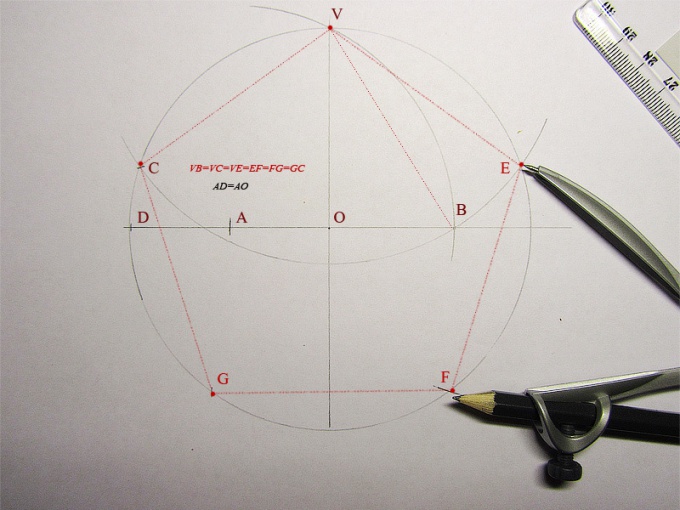
You first need to build the compass circle. The center of the circle may coincide with point O. draw the axis of symmetry perpendicular to each other. At the intersection of one of these axes with the circle put a point V. This point will be the pinnacle of the future Pentagon. At the intersection of the other axis with the circle place the point D.
2
On the segment OD, find the middle and mark it point A. then you need to build a compass a circle with center at that point. In addition, it must pass through the point V, that is, the radius of CV. The point of intersection of the axis of symmetry and the circle label for V.
3
Then, using the compass , swipe a circle of the same radius by placing a needle in the point V. the Intersection of this circle with the original label as a point F. This point will be the second top right of the future Pentagon.
4
Now we need to make the same circle through the point E, but with the center at the Intersection of F. only that the circle with the original label as a point G. This point will become a vertex of the Pentagon. Likewise, to build another round. Its center at G. the Point of intersection of its circumference with the original let it be H. This is the last vertex of a regular polygon.
5
You should have five vertices. Do they just connect on the line. As a result of all these operations you will get inscribed in a circle right Pentagon.
Useful advice
In this simple way, it is possible to construct a Pentagon. To build the triangle, you must spread the legs of the compasses at a distance equal to the radius of the circle. Then at any point install the needle. Fine auxiliary circle. Two points of intersection of the circles and the point at which was the compasses formed by the three vertices of the triangle.