Instruction
1
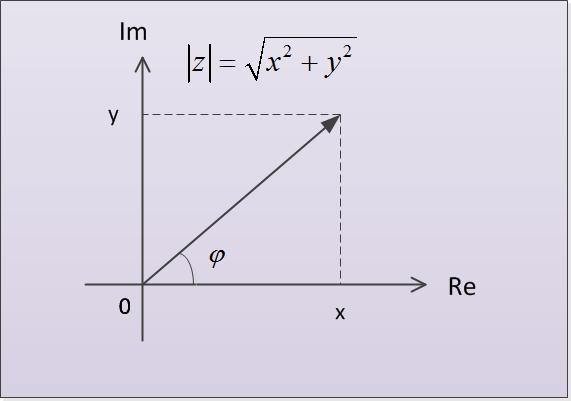
The plane, which is a complex numbercalled complex. On this plane the horizontal axis is the real number (x) and the vertical axis is the imaginary number (y). On this plane number is defined by two coordinates z = {x, y}. In polar coordinates the coordinates of the point are the module and argument. The module is called the distance |z| from the point to the origin. The argument is called the angle ϕ between the vector connecting the point and the origin and horizontal axis of the coordinate system (see figure).
2
The figure shows that the modulus of the complex number z = x + i * y is the Pythagorean theorem: |z| = √ (x^2 + y^2). Further, the argument of the number z is the acute angle of the triangle using the TRIG functions sin, cos, tg:sin ϕ = y / √ (x^2 + y^2),
cos ϕ = x / √ (x^2 + y^2),
tg ϕ = y / x.
3
For example, suppose that the number z = 5 * (1 + √3 * i). First, select a real and imaginary part: z = 5 +5 * √3 * i. It turns out that the real part of x = 5, and the imaginary part y = 5 * √3. Calculate the module number: |z| = √(25 + 75) = √100 =10. Next, find the sine of the angle ϕ: sin ϕ = 5 / 10 = 1 / 2. This leads to the argument of the number z equal to 30°.
4
Example 2. Let the number z = 5 * i. The drawing shows that the angle ϕ = 90°. Check this value in the formula given above. Record the coordinates of the given number in the complex plane: z = {0, 5}. Module number |z| = 5. The tangent of the angle tg j = 5 / 5 = 1. It follows that ϕ = 90°.
5
Example 3. Suppose you want to find the argument of the sum of two complex numbers z1 = 2 + 3 * i, z2 = 1 + 6 * i. According to the rules of addition put these two complex numbers: z = z1 + z2 = (2 + 1) + (3 + 6) * i = 3 + 9 * i. Then as above counting argument: tg ϕ = 9 / 3 = 3.