Instruction
1
Hyperbole in the same way as other curves can be constructed in two ways. The first of these is to build on the rectangle, and the second - on the graph of the function f(x)=k/x.
Begin to build a hyperbole should construct a rectangle with the ends on the x-axis, referred to as A1 and A2, and with the opposite ends of the y-axis, referred to as B1 and B2. Guide the rectangle through the center of the coordinates, as shown in figure 1. The sides should be parallel and equal in magnitude as A1A2 and B1B2. Through the center of the rectangle, i.e. the origin, draw two diagonal guidelines. Dragging these diagonally, you get two lines which are the asymptotes of the graph. Build one branch of the hyperbola, and then, in the same way, and opposite. The function is increasing on the interval [a;∞]. Therefore its asymptotes are: y=bx/a; y=-bx/a. The equation of the hyperbola will look as follows:
y =b/a √ x^2 -a^2
Begin to build a hyperbole should construct a rectangle with the ends on the x-axis, referred to as A1 and A2, and with the opposite ends of the y-axis, referred to as B1 and B2. Guide the rectangle through the center of the coordinates, as shown in figure 1. The sides should be parallel and equal in magnitude as A1A2 and B1B2. Through the center of the rectangle, i.e. the origin, draw two diagonal guidelines. Dragging these diagonally, you get two lines which are the asymptotes of the graph. Build one branch of the hyperbola, and then, in the same way, and opposite. The function is increasing on the interval [a;∞]. Therefore its asymptotes are: y=bx/a; y=-bx/a. The equation of the hyperbola will look as follows:
y =b/a √ x^2 -a^2
2
If instead of a rectangle use square, get ravnovesnaya hyperbole, as in figure 2. Its canonical equation has the form:
x^2-y^2=a^2
Have ravnovesnoi hyperbola the asymptotes are perpendicular to each other. In addition, between y and x have a proportional relationship, namely that if x be reduced in a specified number of times, then y will increase by the same factor, and Vice versa. So, in other words the equation of the hyperbola written in the form:
y=k/x
x^2-y^2=a^2
Have ravnovesnoi hyperbola the asymptotes are perpendicular to each other. In addition, between y and x have a proportional relationship, namely that if x be reduced in a specified number of times, then y will increase by the same factor, and Vice versa. So, in other words the equation of the hyperbola written in the form:
y=k/x
3
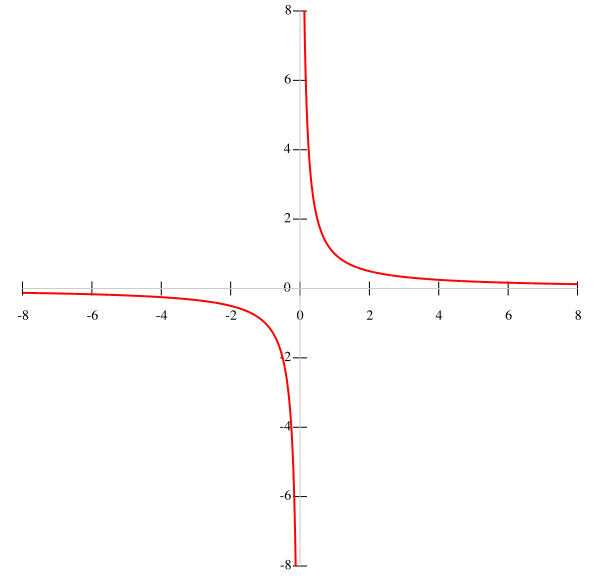
If the condition function is given by f(x)=k/x, it is better to construct a hyperbola by points. Given that k is constant, and the denominator, x≠0, we can conclude that the graph of the function passes through the origin. Accordingly, the intervals of the function is (-∞;0) and (0;∞), because when you call x to the zero function loses its meaning. With increasing x the function f(x) decreases, and with decreasing increases. When approaching x to zero the condition y→∞. The graph of the function shown on the main picture.
4
To build the hyperbola by means of calculation it is convenient to use the calculator. If he is able to work with the program, or at least memorize the formula, you can get him to carry out the calculation several times (number of points) without having to type the expression each time. More convenient in this sense, the graphing calculator, which will take, in addition to calculating and plotting.