How to build a hyperboloid

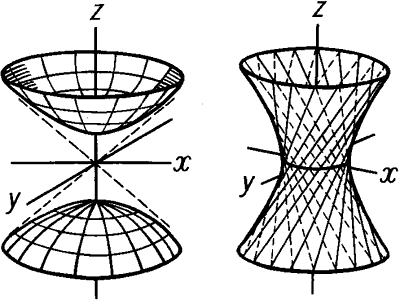
Imagine that there is hyperbole and there is some line that passes through the origin. If a hyperbola to rotate around this axis, there is a hollow rotational body, which is called a hyperboloid. There are two kinds of hyperboloids: odnopodezdny and duopolistic. Odnopodezdny hyperboloid defined by the equation:x^2/a^2 +y^2/b^2-z^2/c^2=1if to consider this spatial figure relative to the planes Oxz and Oyz, it is possible to notice that the main sections are hyperbolas. However, section one-sheet hyperboloid by the plane Oxy is an ellipse. The smallest ellipse of the hyperboloid is called the throat ellipse. In this case, z=0, and the ellipse passes through the origin. The equation of the throat of the ellipse at z=0 can be written as follows:x^2/a^2 +y^2/b^2=1Остальные ellipses have an equation of the following form:x^2/a^2 +y^2/b^2=1+h^2/c^2, where h is the height of the one-sheet hyperboloid.

The construction of the hyperboloid start with the image of the hyperbola in the plane Xoz. Acartia valid axis, which coincides with the y-axis and an imaginary axis coincident with the z. Construct a hyperbola, and then set a certain height h of the hyperboloid. After that, at the level of a given height, draw straight, parallel to Ox, and crosses the graph of the hyperbola in the upper and lower points.Similarly in the plane Oyz construct a hyperbola, where b is the real axis passing through the y-axis and with the imaginary axis is also coincident with c.Build in the plane Oxy of the parallelogram, which is obtained by connecting points of the graphs of hyperbole. Draw the throat ellipse so that it was inscribed in the parallelogram. Similarly build the rest of the ellipses. The result is a drawing of the body of rotation - the one-sheet hyperboloid, shown in Fig.1

Duopolistic hyperboloid got its name because of the two different surfaces, which are formed by the axis Oz. The equation of this hyperboloid is of the form:x^2/a^2 +y^2/b^2 -z^2/c^2=-1Две cavity are obtained when constructing a hyperbola in the plane Oxz and Oyz. Doolotova have a hyperboloid cross section ellipse:x^2/a^2-y^2/b^2=h^2/c^2-1Также, as in the case of one-sheet hyperboloid, build in the planes Oxz and Oyz hyperbole that will be so located, as shown in figure 2. Build upstairs and downstairs parallelograms to construct the ellipses. Constructing ellipses, remove any projection of the building, and then draw duopolistic hyperboloid.