How to find tangential acceleration

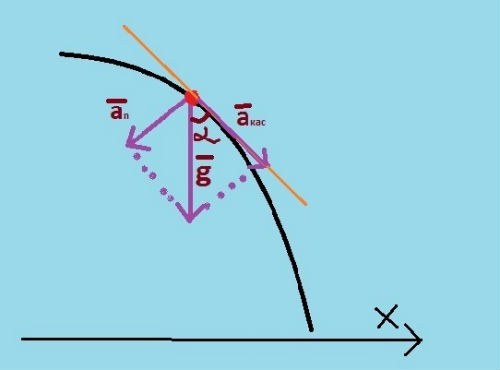
Find the tangential acceleration aτ, if you know the full acceleration of a particle moving along a curved trajectory a and its centripetal acceleration an. To do this, from the square full acceleration, subtract the square of the centripetal acceleration, and from this value, extract the square root aτ=√(a2-an2). If you do not know the centripetal acceleration, but there is a value of instantaneous speed, measure with a ruler or tape measure the radius of curvature of the trajectory and find its value by dividing the square of the instantaneous velocity v, which measure the speedometer or the radar on the radius of curvature of the trajectory R, an=v2/R.

Example. The body moves in a circle with a radius of 0.12 m. Its full acceleration is 5 m/S2, determine its tangential acceleration, at a time when its velocity is 0.6 m/s. First, find the centripetal acceleration of a body at a specified speed, it it square divide by the radius of the trajectory of an= v2/R= 0,62/0,12=3 m/S2. Find the tangential acceleration by the formula aτ=√(a2-an2)=√(52-32)=√(25-9)= √16=4 m/S2.

Find the magnitude of tangential acceleration through a change in the speed module. To do this using a speedometer or radar, determine the initial and final velocity of the body for a certain period of time, which you measure with a stopwatch. Find the tangential acceleration, v the ultimate subtracting from the initial value of speed v0 and dividing the time interval t during which that change occurred: aτ= (v-v0)/t. If the value of the tangential acceleration turned negative, so the body slows down, if positive accelerating.

Example. 4 with the velocity of a body moving along the circumference, decreased from 6 to 4 m/s. Determine the tangential acceleration. Calculated by applying the formula, obtain aτ= (v-v0)/t=(4-6)/4=-0,5 m/S2. This means that the body slows down with an acceleration of the absolute value of which is equal to 0.5 m/S2.