You will need
- The range for plotting ellipses, pencil, eraser.
Instruction
1
As the original shape, use the ellipse with major radius a and minor radius b, as shown in figure 1. If you take the distance AB is equal to 2a, and the distance DC is equal to 2b and rotate an ellipse around one of these axes, we can obtain an ellipsoid of rotation. In General, the ellipsoid obtained by deformation of the sphere along three mutually perpendicular axes. He refers to the surfaces of the second order. The canonical equation of this shape is:x^2/a^2+y^2/b^2+z^2/c^2=1.Sections of the plane Oxz, Oxy, Oyz are ellipses. There are three types of ellipsoids: triaxial, ellipsoid of rotation and a sphere. Have a triaxial ellipsoidand all axles are different, and the ellipsoidof rotation and is equal to only two axle shafts. The sphere has all of the axles are of equal value. The construction of all three types of ellipsoids is on the same circuit. The equation of the ellipsoidof rotation and has the form:x^2/a^2+y^2/ a^2+z^2/c^2 =1.The sphere has all of the semi-axis are equal (a=b=c), and its equation is:x^2+y^2+z^2=1.A triaxial ellipsoid is described by the standard equation :x^2/a^2+y^2/b^2+z^2/c^2=1.
2
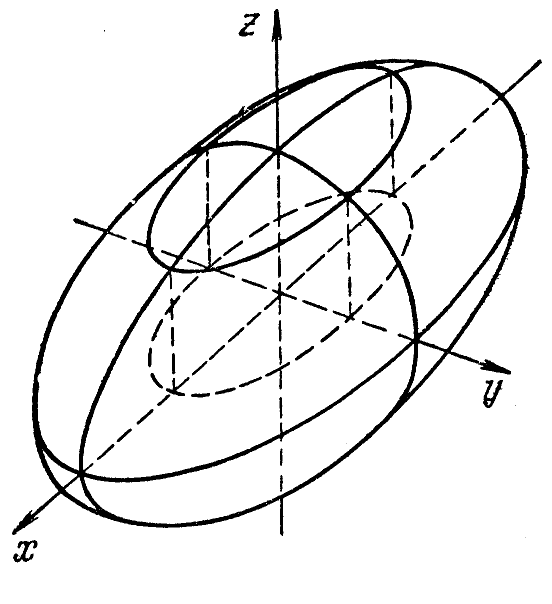
To build the ellipsoid you lofted, first review the equations describing each of the planes [ z=0 plane Oxy (section - an ellipse with semi-axes a and b); [ x^2/a^2+y^2/b^2=1. [ y=0 plane Oxz (section - an ellipse with semiaxes a and C); [x^2/a^2+z^2/c^2=1. [ x=0 plane Ozy (the cross section is an ellipse with the semiaxes b and c) [y^2/b^2+z^2/c^2.
3
Having cross sections of different sizes, build in all three planes ellipses. Will a triaxial ellipsoid. Draw the three-dimensional coordinate system with center at point O. Initially build the ellipse in the plane Oxy. To do this, draw an auxiliary parallelogram, and which enter the ellipse. Similarly draw the other two ellipse in the plane Oxz and Ozy. After all ellipses are drawn, erase all auxiliary parallelograms. It now remains to outline around all three ellipses a common line to portray the surface of the ellipsoid. Invisible lines can also be erased, and visible to leave. In the same way it is possible to build an ellipsoid of rotation and a sphere. Sphere in appearance is a hollow sphere.