How to build a spiral

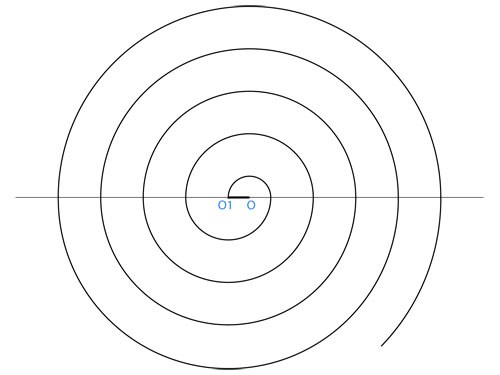
The simple spiral in the drawing can be obtained by moving the centers of the semicircle from one center of the spiral to another. The part is simple to construct and has equal step increase of the radius of the coils. To build label on a sheet of paper or the drawing the center of the spiral O.

Through the center of the spiral, draw a horizontal straight line. Its length on each side from the centre must be greater than or equal to the maximum radius of the spiral.

Note on the direct point at a distance from the center O, which is equal to the minimum radius of the spiral. This is the second center of the spiral, which needed for its construction. Denote it as O1.

From the center O of the spiral guide compass arc, which is a half circle. Arc starts from the circle center O1, and the ends through 180 degrees, the company built a horizontal straight line. The radius of the arc equal to the minimum radius of the spiral.

Set the compass size, equal to two minimum radii of the spiral, and set his leg with the sharp tip of the second center of the spiral - O1. Draw a arc that starts at the point which ended the first arc, and the ends, reaching the horizontal line on the opposite side of the center of the spiral O.

Similarly do the third and subsequent necessary steps of building a spiral. The radius of the semicircle to the third step should be equal to the minimum radius of the spiral loop, multiplied by 3. The radius of the arc for the next steps is equal to the number of construction steps, which multiplied by the minimum radius of the spiral loop.