Instruction
1
If PCF f(z) is analytic in ring 0
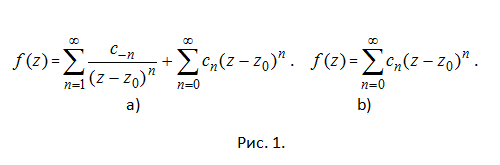
2
If all the coefficients of the Laurent series are zero, then the singular point z0 is called disposable singular point of the function. The decomposition of the Laurent series in this case has the form (Fig. 1b). If the main part of the Laurent series contains a finite number k of terms, then the singular point z0 is called a pole of the k-th order of the function f(z). If the main part of the Laurent series contains an infinite number of members, then a special point is called the essential singular point of the function f(z).
3
Example 1. A function w=(z-2)/[((z-3)^2)z((z+1)^3)] has the singular points: z=3 – pole second order, z=0 pole of the first order, z=-1 is a pole of the third order. Please note that all the poles are found by finding the roots of the equation ((z-3)^2)z((z+1)^3)=0.
4
Deduction of analytic functions f(z) in a punctured neighbourhood of a point z0 is called the coefficient of s(-1) in the expansion of functions in Laurent series. Is denoted by res[f(z), z0]. Given the formula of calculation of coefficients of the Laurent series, in particular, the coefficient C(-1) is obtained (see Fig. 2). Here γ is some piecewise smooth closed contour bounding odnofaznye the region that contains the point z0 (for example, a circle of small radius with center at z0), and lying in a ring 0
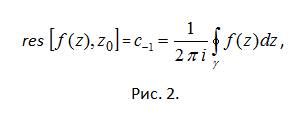
5
So, to find the deduction function in an isolated singular point should either expand the function in a Laurent series and to determine from this decay the ratio s(-1), or calculate the integral of figure 2. There are other ways of calculating deductions. So, if the point z0 is a pole of order k of the function f(z), then a deduction at this point is calculated by the formula (see Fig.3).
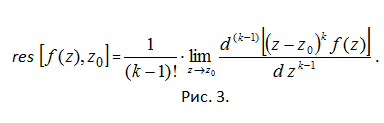
6
If the function f(z)=φ(z)/ψ(z), where φ(z0)≠0, and ψ(z) has a simple root (multiplicity one) at z0, then ψ’(z0)≠0 and z0 is a simple pole of f(z). Then res[f(z),z0]= φ(z0)/ψ’(z0). This rule quite clearly, the conclusion follows. The first thing that is done by finding the singular points is the determination of the roots of the denominator of ψ(z).
Note
Training the mind never puts. Especially for those who are not so used to working with numbers, and especially with roots. Addition and subtraction of roots - a good workout for the bored mind. You cannot add or subtract expressions with different radical expressions. The addition of roots requires compliance with this rule.
Useful advice
Addition and subtraction of roots. For adding and subtracting roots connect them by means of signs of these actions. Then give the roots to simplest form, and if the roots will be like, then make a cast. This Ghost is that the coefficients of like terms, taken from signs of the relevant members, in parentheses, and the common root is removed the brackets multiplier. Then, the resulting General ratio...
