You will need
- a pair of compasses;
- - the range;
- pencil.
Instruction
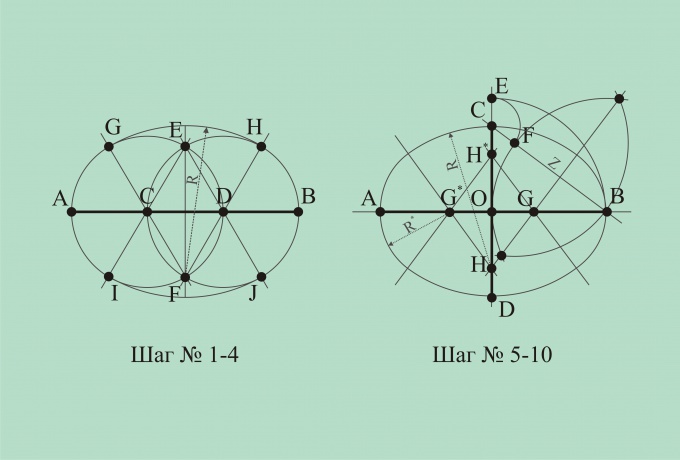
1
Let us known width of the ellipse, i.e. its horizontal axis. Construct the segment AB, different horizontal axis. Divide this line segment into three equal parts by the points C and D.
2
From points C and D as centers construct of a circle with radius equal to the distance between points C and D. the point of intersection of the circles will be denoted by letters E and F.
3
Join the points C and F, D and F, C and E, D and E. These lines intersect the circle at four points. Call these points G, H, I, J, respectively.
4
Note that the distance EI, EJ, FG, FH are equal. Let us denote it as R. the distance From point E as the center will draw an arc of radius R connecting the points I and J. connect the points G and H arc of radius R with center at the point F. Thus, the oval can be considered built.
5
Now let known to the length and width of the oval, i.e. both axes of symmetry. We will have two perpendicular lines. Let these lines meet at point O. On the horizontal line put the segment AB with center at point O, equal to the length of the oval. On the vertical line put the segment CD with center at point O, equal to the width of the oval.
6
Direct connect points C and B. From the point O as the center will draw an arc of radius OB, connecting the lines AB and CD. The point of intersection with the straight line CD will be called point E.
7
From point C draw an arc of radius CE so that it crosses the line segment CB. The point of intersection denoted by point F. the Distance FB will be denoted by Z. From the points F and B as centers we will have two crossing arcs with a radius of Z.
8
Connect the point of intersection of the two arcs straight and call the point of intersection of this line with the axes of symmetry points G and H. Put G-spot* the G-spot is symmetrical relative to the point O. And mark point H* symmetrical point H relative to point O.
9
Connect points H and G*, H* and G*, H* and G are straight lines. Denote the distance HC as R, and the distance GB as R*.
10
From the point of H as centre, draw the arc of radius R intersecting the straight HG and HG*. From point H* of center, draw the arc of radius R intersecting the straight H*G* and H*G. From points G and G* as from the centres will hold the arc of radius R*, closing the resulting figure. The construction of the oval is finished.