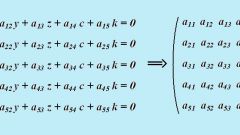As from the matrix to build a graph

The graphs are oriented and undirected. In the first case, the edges connecting the graph nodes, set the direction of movement arrow at one of their ends. If the edge starts and ends at the same vertex, it degenerates into a loop. All these terms count explicitly defined in the matrix of incidence. Matrix seinasta only contains information about the connectivity between vertices in the graph, without revealing its features.

Build the count matrix incindence. To do this, count the number of rows n and columns m in a given matrix. The rows correspond to vertices and columns to edges. Free paper space, select the vertices of the construction graph circles, there will be as many lines contains the matrix of incidence. Number the vertices from 1 to n.

The analysis of the matrix should be made according to the columns, thus determining the existence of a relationship between vertices and its direction. Examining the first column from top to bottom, looking for a value different from zero. While the number of -1 or 1 will remember which line it is located, and look for the second unit in the same column. Find both numbers, swipe to graph a line connecting two vertexes marked lines. If one of the found values was -1, so the graph is cluster – specify on the line guide the arrow to the top where the matrix is -1. If both values are described by the units thus constructed an undirected graph and its edges have no direction. If the detected column number 2, draw a loop at the vertex corresponding to the positional row of the matrix. Zero values indicate a lack of connection. Consider similarly the other columns and display the picture all the given edges of the graph.

Build a graph on the adjacency matrix. This matrix is square since the number of rows equal to the number of columns and corresponds to the number of vertices in the graph. On a sheet draw circles show peaks in the number of the period matrix. The analysis of the adjacency matrix is best done by moving along the line. Starting from the first row from left to right, looking for values other than zero. Finding 1 (or other nonzero number) note the current position in the row and column. On the graph draw a line between the vertices corresponding to observed row and column. Ie, if 1 is at the intersection of 2 rows and 3 columns of the adjacency matrix, the graph edge connects 2 and 3 of its vertices. Continue the search for non-zero values to the end of the adjacency matrix and complete graph in the same way.