How to find the center of gravity of the body

If the body's center of gravity which you want to define homogeneous and has a simple rectangular shape, round, spherical, cylindrical, square, and has a center of symmetry, in such a case, the center of gravity coincides with the center of symmetry.

For a homogeneous rod the center of gravity is in its middle, that is, in its geometric center. The same result is obtained for the uniform circular disk. Its centre of gravity lies at the point of intersection of the diameters of the circle. Therefore, the center of gravity of the Hoop will be in the center, outside points of the Hoop. Find the center of gravity of a homogeneous sphere is at the geometric center of the sphere. The center of gravity of a homogeneous rectangular parallelepiped will be at the intersection of its diagonals.

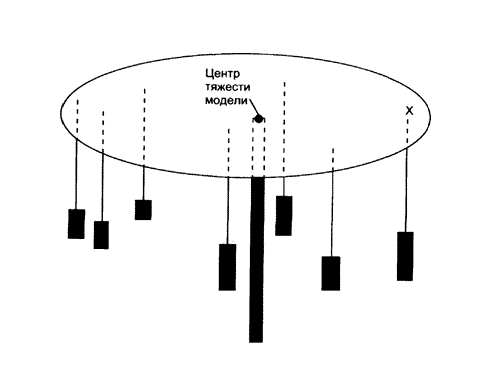
If the body has arbitrary shape if it is patchy, for example, has recesses to calculate the position of the center of gravity difficult. See where such a body is the point of intersection of all forces of gravity that act on this figure when it is turning. To find this point is the easiest experimentally using the method of free suspension of the body on the thread.

Consistently attach the body to the filament for different points. At equilibrium the centre of gravity of body must lie on a line coinciding with the line of thread, otherwise gravity brings the body in motion.

Using a ruler and pencil draw a vertical straight coinciding with the direction of the filaments, which were attached at different points. Depending on the complexity of body shape will need to spend two to three lines. They must all intersect in one point. This point will be the center of gravity of the body, because the center of gravity must remain on all such lines.

Determine by the method of hanging the center of gravity as flat shapes, and more complex body, the form of which may vary. For example, two bars connected by a hinge, in the unfolded state have the center of gravity at the geometric center, and in a bent – their center of gravity is outside these bars.