You will need
- The value of the radius of the circle diameters, the value of the constant π.
Instruction
1
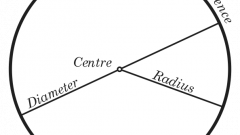
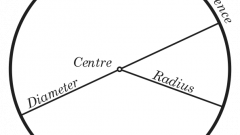
First you have to analyze the source data to the task. The fact that her condition cannot be explicitly said, what is the length of the radius of the circle. Instead, the task can be given to the length of the diameter of the circle. The diameter of a circle - a segment that connects two opposite points of the circlepassing through its center. After analyzing the definitions of circumference and diameter, we can say that the length of the diameter is twice the radius length.
2
You can now take the radius of a circle is equal to R. Then to find the length of a circle you must use the formula:
L = 2nr = πD, where L is the length of the circumference, D is the diameter of a circle, which is always 2 times greater than the radius.
L = 2nr = πD, where L is the length of the circumference, D is the diameter of a circle, which is always 2 times greater than the radius.
3
You can see an example of the application of the formula: given a circle with diameter 8 cm is Required to find the length of the circumference.
Solution: L = 2*3,14*4 = 3,14*8 = 25,12 cm
Answer: length of a circle with a diameter of 8 cm is equal to 25.12 cm
Solution: L = 2*3,14*4 = 3,14*8 = 25,12 cm
Answer: length of a circle with a diameter of 8 cm is equal to 25.12 cm
Note
A circle can be inscribed in the polygon, or to describe around him. Thus, if the circle is inscribed, it is at the points of tangency with the sides of the polygon will divide them in half. To find the radius of the inscribed circle, divide the area of a polygon is half its perimeter:
R = S/p.
If a circle circumscribed around a triangle, then its radius is set according to the following formula:
R = a*b*c/4S, where a, b, c are the sides of this triangle, S is the area of a triangle around which a circle is described.
If you want to describe a circle around the quadrilateral, then it can be done if two conditions are met:
The quadrilateral must be convex.
In the sum of opposite angles of a quadrilateral must be 180°
R = S/p.
If a circle circumscribed around a triangle, then its radius is set according to the following formula:
R = a*b*c/4S, where a, b, c are the sides of this triangle, S is the area of a triangle around which a circle is described.
If you want to describe a circle around the quadrilateral, then it can be done if two conditions are met:
The quadrilateral must be convex.
In the sum of opposite angles of a quadrilateral must be 180°
Useful advice
In addition to the traditional Vernier caliper, for drawing circle you can use stencils. Modern stencils included the circumference of different diameters. These stencils can be purchased at any office supply store.