Instruction
1
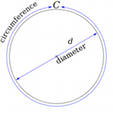
If you know the diameter of the circle (D), to calculate the length of circumference (L) multiply this value by PI: L=π*d. the constant (PI) and was introduced by mathematicians as a numeric expression is a constant ratio between the circumference and its diameter.
2
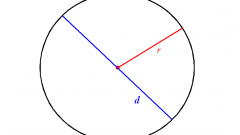
If you know the radius of the circle (R), it is possible to replace the only variable in the formula from the previous step. Since the radius is by definition equal to half the diameter, the formula and bring to this type: L=2*π*R.
3
If you know the area of the plane (S) enclosed within the perimeter of the circle, this parameter uniquely identifies the length of the circumference (L). Extract the square root of the product of the square by PI, and the result is double: L=2*√(π*S).
4
If the circle is not known, but available data rectangle, which is inscribed in this figure, it can be enough to calculate the circumference of a circle. Because the only rectangle in which it is possible to inscribe a circle is a square, the diameter of the circle and side length of the polygon (a) coincide. Use the formula from the first step, replacing in it the diameter a side length of the square: L=π*a.
5
If the length of the sides is described about the circumference of the rectangle is unknown, but in terms of the problem given the length of its diagonal (c), for finding the circumference of a circle (L) use the Pythagorean theorem. From this it follows that the side of the square is equal to the ratio between the diagonal length and the square root of two. Substitute this value into the formula from the previous step and it will become clear that, to find the circumference of a circle you need the product of length of diagonals in PI divided by the square root of two: L=π*s/√2.
6
If the circle is circumscribed around a regular polygon with any number of vertices (n), then for finding the perimeter of a circle (L) will be sufficient to know the length of a side of the inscribed figure (b). Divide the length of the side to twice the sine of PI divided by the number of vertices of the polygon: L=b/(2*sin(π/n)).
Note
A circle is a closed plane curve, all points of which are equidistant from a point (center of circle), lying in the same plane as the curve itself.The circle is the part of the plane bounded by a circle. The radius of a circle is the segment that connects the center of the circle with any point.
Useful advice
Circle — a closed plane curve, all points of which are equidistant from a given point (center) lying in the same plane as the curve. Circle the part of the plane bounded by a circle. The diameter always passes through the center of the circle. Is usually denoted by D or Ø. The diameter is twice the radius of the circle: D = 2R R = D/2. The ratio of a circle's circumference to its diameter is the same for all circles.