Instruction
1
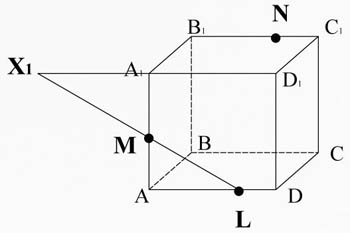
Suppose that we are given cube ABCDA1B1C1D1. It is necessary to conduct a cross-section through points M, N and L, lying on his ribs.
Connect points L and M. the Direct ML and the edge A1D1 lie in the same plane ADA1D1. Cross them, get the point X1. Cut ML the intersection of the plane of the cross section with the face AA1D1D.
Connect points L and M. the Direct ML and the edge A1D1 lie in the same plane ADA1D1. Cross them, get the point X1. Cut ML the intersection of the plane of the cross section with the face AA1D1D.
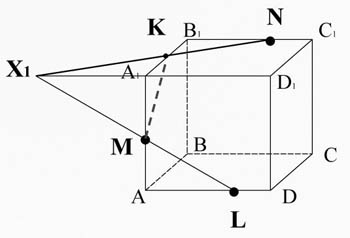
2
A point X1 belongs to the plane A1B1C1D1, t lies on the straight line A1D1. Video X1N A1B1 intersects the edge at point K. a line Segment KM is the intersection of the plane of the cross section with the face AA1B1B.
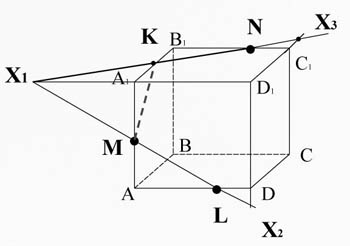
3
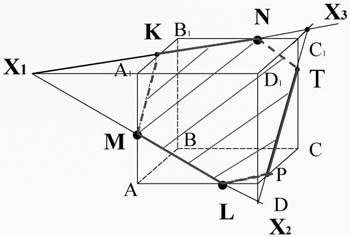
Video ML D1D and the edge lie in the same plane AA1D1D. Cross them, get the point X2. Video KN and edge D1C1 also lie in the same plane A1B1C1D1. Cross them, get the point X3.
4
Build direct X2X3. This line lies on the plane CC1D1D and rib intersects DC at point P, edge CC1 at point T.
By connecting the points L, P, T and N will receive a section MKNTPL.
This way you can build a cross section of any polygonal.
By connecting the points L, P, T and N will receive a section MKNTPL.
This way you can build a cross section of any polygonal.