Instruction
1
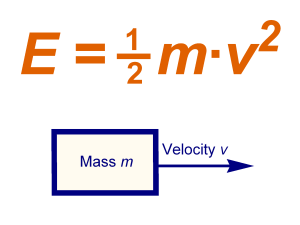
In the case of translational motion all points of the system (body) have the same speed, which is equal to the velocity of the center of mass of a body. While the kinetic energy of the system Tpost equal to:
Tpost = ? (mk Vс2)/2,
where mk is the body mass, VC is the speed of the center of mass.Thus, when the forward movement of the body kinetic energy is equal to the product of body weight to the square of the velocity of the center of mass, divided by two. The value of the kinetic energy does not depend on the direction of movement.
2
In rotational motion, when the body rotates around any axis Oz, the speed of any point determines the equation: Vk = ?hk, where hk is the distance of this point to the axis of rotation ? - the angular velocity of the body. If we substitute the equation that determines the velocity of a point at the expression and make the overall multipliers of the bracket, we will obtain the equation of the kinetic energy of the system while the rotational motion: TVR = ? (mk ?2 hk2)/2 = ? (mk hk2) ?2/2Выражение made in brackets represents the moment of inertia of the body about the axis around which the rotation of the body. Here you will receive: TVR = (Iz ?2)/2, where Iz is the moment of inertia of the body. Thus, when the rotational motion of the body, its kinetic energy is equal to the product of the moment of inertia of the body about the rotation axis to the square of its angular velocity divided in half. The direction of rotation of the body does not affect the value of its kinetic energy.
3
In the case of a perfectly rigid body is full of kinetic energy is equal to the sum of the kinetic energies of translational and rotational motion:T = (mk Vc2)/2 + (Iz ?2)/2