Instruction
1
To translate octal numbers into the binary system need every figure be represented in the form of triads of binary digits. For example, the octal number 765 decomposed into triads as follows: 7 = 111, 6 = 110, 5 = 101. The result is the binary number 111110101.
2
For the translation of hexadecimal numbers to a binary system of notation you need every figure to represent a tetrad of binary digits. For example, the hexadecimal number 967 decomposed into tetrads as follows: 9 = 1001, 6 = 0110, 7 = 0111. The result is the binary number 100101100111.
3
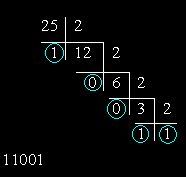
To translate a decimal number in the binary system of notation, it is necessary to divide it into two, each time recording the result in the form of a whole number and a remainder. The division must continue until, until the number is equal to one. The total number is obtained by consistent recording of the result of the last division and remainders of all divisions in reverse order. As an example, the figure shows the procedure of decimal number 25 in the binary system of notation. Successive division by two gives the following residue sequence: 10011. Deploying it on the contrary, obtain the required number.
Note
Therefore, having a series of multiplications by 2 to the right of the vertical zeroes, we finish the process of translating a decimal number less than one in the binary number system and record the response: it is Clear that the more often we meet such a source decimal when multiplying by 2 digits, standing on the right from the vertical will not result in there only zeros.
Useful advice
We already know how to translate numbers in different number systems. Let's see how this happens with the binary number system. Let's convert the number from binary to decimal. So was invented the octal and hexadecimal systems scaleni. They are comfortable as decimal numbers that represent the number requires fewer digits. As compared to decimal numbers, binary representation is very simple.

