How to define the work in an isothermal process

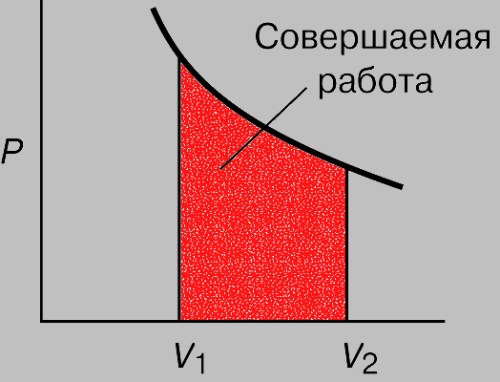
Calculate work of gas at a constant temperature. This will determine which gas performs work, and calculate its molar mass. Using the periodic table to find molecular mass, which is numerically equal to molar mass, measured in g/mol.

Find the mass of gas. To do this, vent the air from the sealed container and weigh it on the scale. After that extract the gas, which is determined, and again weigh the container. The difference between the masses of the empty and filled vessel and is equal to the mass of gas. Measure it in grams.

Measure with a thermometer the temperature of the gas. In isothermal process it will be permanent. If the measurement is performed at room temperature, it is sufficient to measure the temperature of the surrounding air. Measurements are produced in Kelvins. For this, the temperature measured in degrees Celsius, add 273 to the number.

Determine the initial and final gas volume in operation. To do this, take a vessel with a movable piston, and computing the level of his ascent, calculate the primary and secondary volume of geometric methods. To do this, use the formula for volume of a cylinder V=π•R2•h, where π≈3,14, R is the radius of the cylinder, h its height.

Calculate work of gas in an isothermal process. To do this, divide the mass of gas m its molar mass M. Polecany multiply the result by the universal gas constant R=8.31 and the temperature T in Kelvin. The result multiply by the natural logarithm of the ratio of final and initial volumes V2 and V1, A = m/M•R•T•ln(V2/V1).

In the case where the known quantity of heat Q, which received the body in an isothermal process, use the second law of thermodynamics Q = ∆U + A. Where A is the working gas, ΔU is the change in its internal energy. Since the change in internal energy depends on temperature, and at isothermal process remains constant, then ΔU=0. In this case, the working gas is equal to the heat transferred to it Q = A.