You will need
- Know of sides of the polygon, its area/perimeter.
Instruction
1
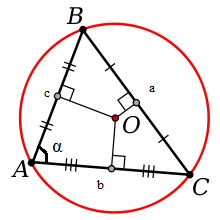
The calculation of the radius of the circumscribed around the triangle of the circle.
If a circle circumscribed around the triangle with sides a, b, c, area S and angle ?, lying up against the side a, the radius R can be calculated by the following formulas:
1) R = (a*b*c)/4S;
2) R = a/2sin?.
If a circle circumscribed around the triangle with sides a, b, c, area S and angle ?, lying up against the side a, the radius R can be calculated by the following formulas:
1) R = (a*b*c)/4S;
2) R = a/2sin?.
2
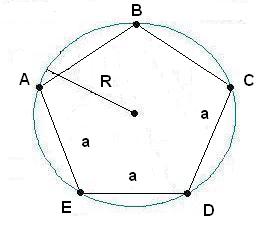
The calculation of the radius of a circlecircumscribed around a regular polygon.
To calculate the radius of a circlecircumscribed around a regular polygon, you need to use the following formula:
R = a/(2 x sin (360 / (2 x n))) where
a - side of a regular polygon;
n is the number of sides.
To calculate the radius of a circlecircumscribed around a regular polygon, you need to use the following formula:
R = a/(2 x sin (360 / (2 x n))) where
a - side of a regular polygon;
n is the number of sides.
Note
Around a polygon, you can describe a circle only if it is regular, i.e. all its sides equal and all its angles equal.
The thesis, which States that the center of the circumscribed around the circumference of the polygon is the intersection of its middle perpendiculars are valid for all regular polygons.
The thesis, which States that the center of the circumscribed around the circumference of the polygon is the intersection of its middle perpendiculars are valid for all regular polygons.