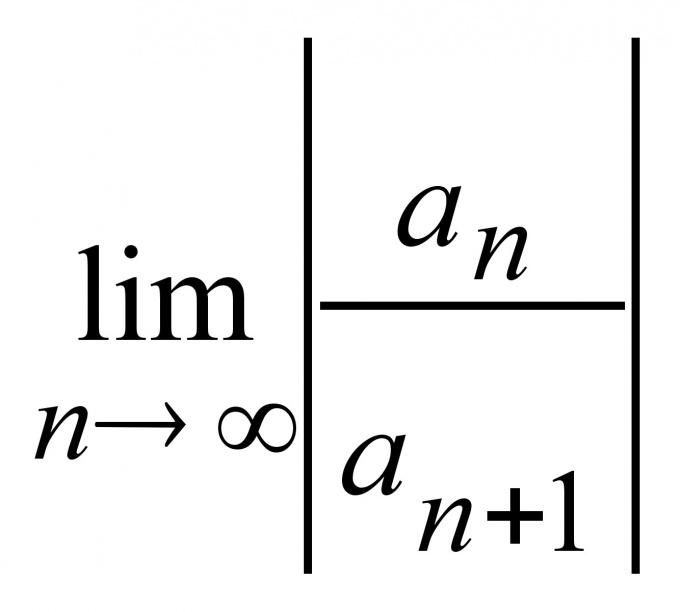How to find the region of convergence of the series

Let's consider a given numerical series U0 + U1 + U2 + U3 + ... + Un + ... = ∑Un. Un expression for a General member of this series.
Summing up the members number from the beginning up to some finite n, you get the Subtotal row.
If with increasing n, these sums tend to a finite value, the series is called convergent. If they rise or fall indefinitely, then the series diverges.

To determine whether a given convergent series, first check, is it a common member of Un to zero under the infinite increase of n. If this limit is not zero, the series diverges. If equal, then the series may convergent.For example, the number of powers of two: 1 + 2 + 4 + 8 + 16 + ... + 2^n + ... is divergent, since its General term in the limit tends to infinity.The harmonic series 1 + 1/2 + 1/3 + 1/4 + ... + 1/n + ... diverges, while its total member and tends in the limit to zero. On the other hand, a number of 1 + 1/2 + 1/4 + 1/8 + ... + 1/(2^n) + ... converges, and the limit of the sum is equal to 2.

Suppose we are given two series, shared members, which are, respectively, Un and Vn. If there is a finite N, since it is, Un ≥ Vn, then these series can be compared. If we know that the series U converges, then the series V is also absolutely right. If it is known that the number of V diverges, then the series U is divergent.

If all members of a series are positive, its convergence can be assessed on the basis of d'alembert. Find the ratio p = lim(U(n+1)/Un) when n → ∞. If p < 1, the series converges. When p > 1, the series clearly diverges, but if p = 1 requires additional study.

If the signs are members of a number of alternate, there are a number has the form U0 - U1 + U2 - ... + ((-1)^n)Un + ..., the series is called the alternating or image. The convergence of this series is determined by the sign of Leibnitz. If the total member of the Un with increasing n tends to zero, and for each n, Un > U(n + 1), then the series converges.

In the analysis of roles often have to deal with power seriesmi. A power series is a function defined by the expression:f(x) = a0 + a1*x + a2*x^2 + a3*x^3 + ... + an*x^n + ...the Convergence of such a seriesnaturally depends on the value x. Therefore, for the power series there is the concept of the range of all possible values of x for which the series converges. This range is equal to (-R; R), where R is the radius of convergence. Inside the series converges always beyond, always at odds, on the border can both converge and diverge.R = lim |an/a(n+1)| when n → ∞.Thus, for the analysis of convergence of the power series is sufficient to find R and check the convergence of the series on the boundary of the range i.e. at x = ±R.

For example, suppose you are given a number that represents a decomposition of the Maclaurin series of the function e^x:e^x = 1 + x + (x^2)/2! + (x^3)/3! + ... + (x^n)/n! + ...The ratio an/a(n+1) is equal to (1/n!)/(1/(n+1)!) = (n+1)!/n! = n + 1. The limit of this ratio as n → ∞ is equal to ∞. Hence, R = ∞ and the series converges on the entire real axis.