You will need
- a blank sheet of paper;
- pencil;
- line;
- textbook on geometry.
Instruction
1
Consider the right triangle ABC, where ∠ABC = 90°. Omit from this angle, the altitude h to the hypotenuse AC, the intersection of the altitude with the hypotenuse denoted by D.
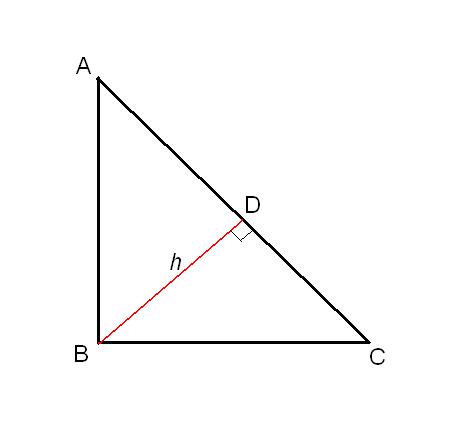
2
Triangle ADB is similar to triangle ABC two angles are: ∠ABC = ∠ADB = 90°, ∠BAD is common. The similarity of triangles we obtain the ratio: AD/AB = BD/BC = AB/AC. Take the first and last ratio, proportion, and we find that AD = AB2/AC.
3
Since the triangle ADB is right angle, for his fair the Pythagorean theorem: AB2 = AD2 + BD2. Substitute in this equality AD. It turns out that BD2 = AB2 - (AB2/AC)2. Or what is the same, BD2 = AB2(AC2-AB2)/AC2. Because the rectangular triangle ABC, AC2 - AB2 = BC2, then get BD2 = AB2BC2/AC2 or, extracting the square root of both sides, BD = AB*BC/AC.
4
On the other hand, also the triangle BDC is similar to triangle ABC two angles are: ∠ABC = ∠BDC = 90°, ∠DCB - General. From the similarity of these triangles we get the aspect ratio of BD/AB = DC/BC = BC/AC. This proportion is expressed through the DC side of the original right triangle. To do this, consider the second equality in proportion and we find that DC = BC2/AC.
5
From the ratio obtained in step 2, have that AB2 = AD*AC. Step 4 have that BC2 = DC*AC. Then BD2 = (AB*BC/AC)2 = AD*AC*DC*AC/AC2 = AD*DC. Thus, the height of BD is the square root of the product of AD and DC, or as they say, the average geometric parts into which the altitude divides the hypotenuse of the triangle.
Note
If the altitude drawn from the vertex with the right angle to the hypotenuse then the triangle is divided into two smaller triangle similar to the original and similar to each other.
Useful advice
In a right triangle, both sides act as the heights.
