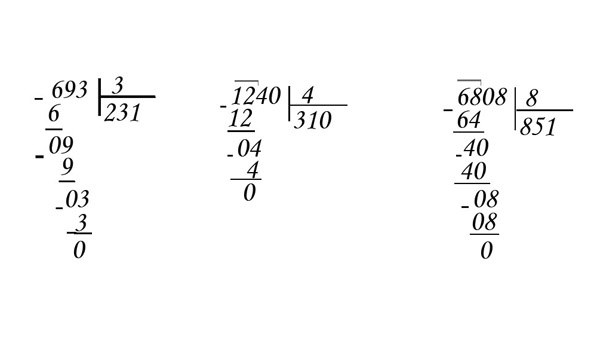You will need
- - handle;
- paper for records.
Instruction
1
First, check the child's skills in multiplication. If the child unsteadily knows the multiplication table, the division he, too, can be a problem. Then in the explanation of the division can be allowed to peek into the crib, but the table still have to learn.
2
Start with the simple division of the number by a digit. Verify that the answer was no residue, otherwise the baby may become confused. Take, for example, 372 and ask to split into 6 parts.
3
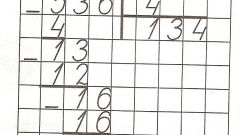
Write the dividend and divisor through the separating vertical line. Under the divider you will write a response - private, separated by a horizontal line. Take the first digit of the number 372 and ask the child how many times the number six "fits" in the top three. Right, not at all.
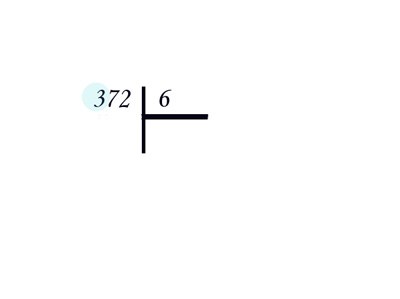
4
Then take the two numbers is 37. For clarity, we can distinguish them in the area. Again repeat the question – how many times the number six contains 37. To count quickly, handy multiplication table. Pick up the answer together: 6*4 = 24 – very unlikely; 6*5 = 30 is close to 37. But 37-30 = 7 – six "fit" again. Finally, 6*6 = 36, 37-36 = 1 – suitable. The first digit of the private – 6. Write it under the divisor.
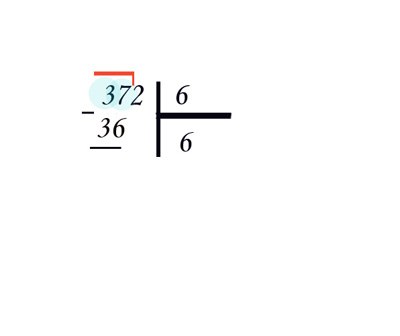
5
36 record under the number 37, move feature. For clarity in the record, you can use the minus sign. Below the line put the remainder of – 1. Now "down" the next digit of the number, two, to unit – turned 12. Explain to your child that the numbers are always "down" one. Again ask how many "sixes" contains 12. The answer is 2, this time without a trace. Write the second digit of the private next to the first. The final result is 62.
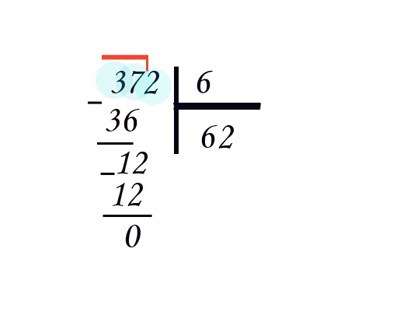
6
Also consider the case of division with remainder. For example, 167/6 = 27 and the remainder is 5. Most likely, your offspring about simple fractions have not heard anything. But if he's going to ask questions, what to do with balance then, you can explain on the example of apples. 167 apples divided among six people. Everyone got 27 pieces and five apples left unshared. You can divide and cut each into six slices and distributing equally. Each person got one slice from each Apple – 1/6. And since apples had five pieces, and the slices each was five or 5/6. That is, the result can be written as: 27 5/6.
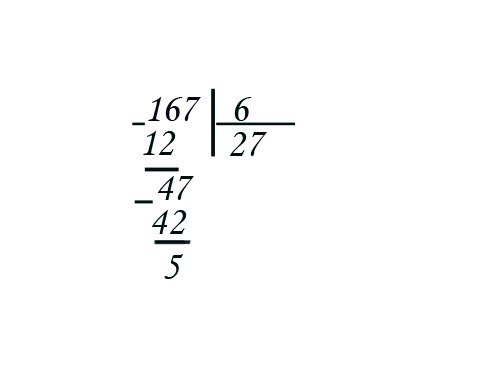
7
To consolidate information take three more examples of division:
1) the First digit of the dividend contains the divisor. For example, 693/3 = 231.
2) the Dividend ends in zero. For example, 1240/4 = 310.
3) the Number contains a zero in the middle. For example, 6808/8 = 851.
In the second case, children sometimes forget to add the last digit of the answer is 0. And in the third, sometimes, jump through zero.
1) the First digit of the dividend contains the divisor. For example, 693/3 = 231.
2) the Dividend ends in zero. For example, 1240/4 = 310.
3) the Number contains a zero in the middle. For example, 6808/8 = 851.
In the second case, children sometimes forget to add the last digit of the answer is 0. And in the third, sometimes, jump through zero.