Instruction
1
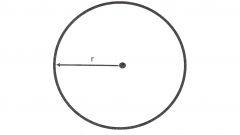
Imagine you are given a circle with known radius R, her L chord subtends an arc φ, where φ is defined in degrees or radians. In this case, calculate the length of the chord according to the following formula: L = 2*R*sin(φ/2), substituting all known values.
2
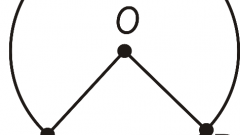
Consider a circle with center at point O and a given radius. Sought are two equal chords AB and AC, having one point of intersection with the circumference (A). It is known that the angle formed by the chords, based on the diameter of the figure. Do the graphical construction of these elements in circumference. The radius from the center Of lower to points of intersection of chords A. Chords will form a triangle ABC. To determine the lengths of the same chords use properties of the isosceles triangle (AB=AC). The segments IN the OS and is (as by the condition - diameter) and are the radii of the figure, therefore, AO is a median of triangle ABC.
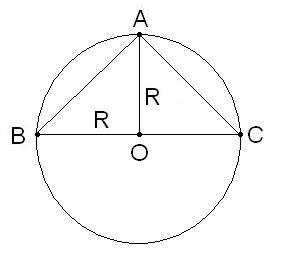
3
According to the property of isosceles triangle, its median is also the altitude, that is, perpendicular to the base. Consider received right triangle AOB. The leg S is known and equal to half the diameter, that is, R. the Second leg of AO is also specified as a radius R. Hence, applying the Pythagorean theorem, Express the unknown side AB, which is the required chord of the circle. Calculate the final result AB = √(AO2 + ОВ2). According to the problem, the length of the second chord AC equal to AB.
4
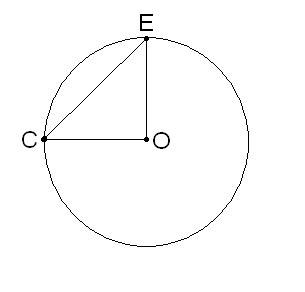
For example, set to a circle with diameter D, and chord CE. Thus the known angle formed by a chord and a diameter. To calculate the length of the chord using the following build. Draw a circle with center at point O and the chord CE, swipe the diameter through the centre and one of the points of the chord (C). It is known that any chord connects two points of the circle. Omit from the second point of intersection with the circle (E) to the center Of the radius EO. Thus, it is an isosceles triangle SEO with the base-chord CE. At a known angle at the base of the eco calculate the chord using the formula from the theorem on projections: CE = 2*a*cos
Useful advice
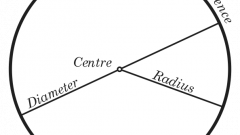
If the chord passes through the center of a circle, it is diameter. The angle between intersecting chords corresponds to the sum of the measures of the arc, located in the corner, and arc in front of her. If the tangent to the circumference, and the chord form an angle, it is equal to the half-degree value of the arc subtended by the same chord.