You will need
- - a sheet of paper;
- - graphite pencil.
Instruction
1
First try to portray a smooth circumference - the Foundation of the ball. In the right part of the page draw a straight line and mark its center point. Through this point guide the same along the length of the line perpendicular to the first. Let the lines will be barely noticeable. You can use the ruler to determine the center, but it is better to learn to use the eye - if you intend to continue to pursue drawing, it will be useful more than once.
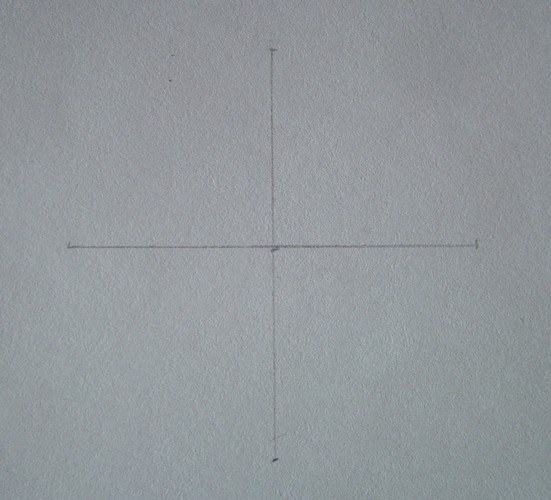
2
Draw a circle, connecting the 4 extreme points of intersecting lines. Don't worry if you can't get even round the first time - just try to draw it until you get it. If necessary, erase the extra lines when the circle is ready.

3
The next stage - the creation of the volume. This is achieved through shadows. For example, light incident from the left and top. Mark the point on the illuminated part of the ball. Touch and mark the width of the shadow.
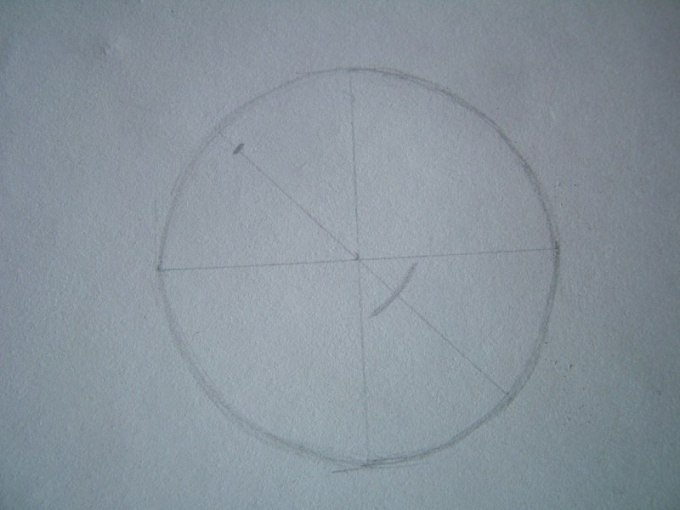
4
Now draw the diameter of the balloonand through its center, perpendicular to the direction of the incident light. On the basis of cut diameter draw an ellipse. Its purpose is to define the boundaries of light and shadow.

5
Conventionally, the ball is divided into several parts depending on the degree of illumination. One part is lit strongly, the other weakly, and the third darker, fourth is in the shade. Label these areas of different light at first thought. For clarity, you can put yourself in front of the eyes of any physical object in the form of a ball. The most lit place that reflect light, called glare. You can just remember or mark on the paper.
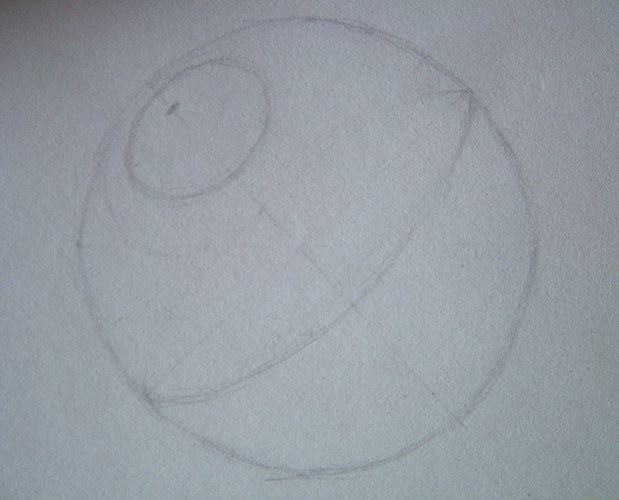
6
Around the highlight will be a bright spot, he is surrounded by the penumbra (gradual transition from light to shadow) and the shadow area. Draw the shadow using curved strokes.
7
Now go on to hatch. If you draw with a pencil, just leave the area of the flare intact. Light area make a light gray, shading becomes darker in the direction of the shadows. Use curved strokes parallel to the contour of the balla, and then diverging radially from highlight to shadow. Note the reflex is lighter compared to the falling shadow (reflex is the reflection from the surface, which is the ball).

8
Draw Cabinet shadow (cast by the Orbohms on surface). The farther from the balland the shadow lighter. In daylight it is less clear, with faux - clearer.

9
If necessary, draw the object plane and the background.

Note
Do not use the eraser too often, so as not to damage the paper. Choose quality soft eraser.
Useful advice
If you've never painted, first practice on the shading and learn how to hold a pencil.
