How to find the perimeter of an octagon

Perimeter of an octagon, just like any other flat geometric shape that is the sum of the lengths of its sides. To solve the problem of determining this parameter of the polygon is sometimes necessary only with use of mathematical formulas, and sometimes to measure them with any means at hand. In any case, the way to solve the problem, there are several and each of them will be optimal for a given set of initial conditions.

How to find the perimeter of an octagon
How to construct a regular octagon
How to find the area of an octagon
How to find the perimeter of a quadrilateral

Instruction

If we calculate the perimeter (P) of an octagon is necessary in theory, but in the original terms of the lengths of all sides of this figure (a, b, c, d, e, f, g, h), add these values: P = a+b+c+d+e+f+g+h. To know the lengths of all sides are necessary only in the case of an irregular polygon, and if the conditions of the problem know that the figure is correct, it will be quite the length of one hand - just increase it eight times: P = 8*a.

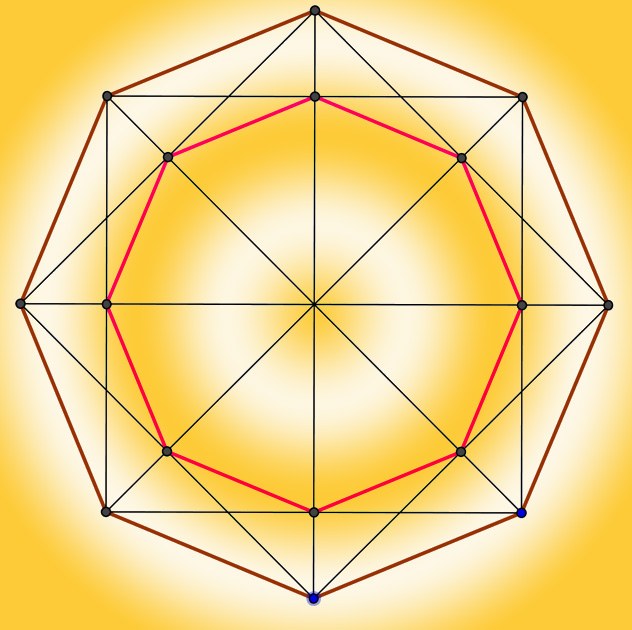
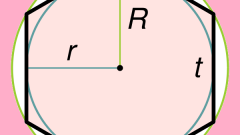
If the original data says nothing about the length of sides of a regular octagon, but given the radius described about the shape of the circle (R), before application of the formula from the previous step will have to calculate the missing variable. Each side of this octagon can be considered an isosceles triangle, the sides of which are radii of the circle. Since most of these similar triangles is eight, the angle between the radii of each of them will be one-eighth part of a complete turn: 360°/8 = 45°. Knowing the lengths of two sides of a triangle and the angle between them, determine the magnitude of base - the cosine of half the angle and multiply by twice the length of the side: 2*R*cos(22,5°) ≈ 2*R* 0,924 ≈ R* 1,848. Substitute the value obtained into the formula from the first step: P ≈ 8*R*1,848 ≈ R*14,782.

If the conditions of the problem given only the radius (r) inscribed in the regular octagon of the circle, it is necessary to perform calculations similar to those described above. In this case, the radius can be represented as one of the legs of a right triangle, the other leg of which is half of the desired side of the octagon. The acute angle adjacent to the radius will be two times less calculated in the previous step: 360°/16 = 22,5°. The length of the right side calculate by multiplying the tangent of that angle on the other side (radius), and to determine the amount of sides of the octagon resulting value double: 2*r*tg(22,5°) ≈ 2*r*0,414 ≈ r*0,828. Substitute this expression into the formula from the first step: P ≈ 8*r*0,828 ≈ r*6,627.

If you calculate the radius required by the method of practical dimensions, depending on the figure size, use, for example, line, odometer ("rolling meter") or a pedometer. The obtained values of the lengths of the sides put in one of the two formulas given in one of the steps.

Is the advice useful?