You will need
- - a sheet of paper;
- - gon;
- pencil;
- a pair of compasses;
- - pattern;
- - eraser;
- calculator.
Instruction
1
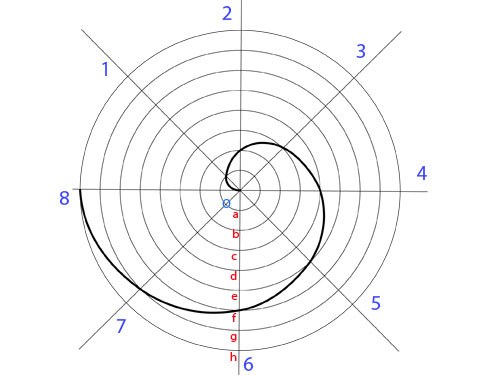
Mark on the drawing point which is the center of the spiral of Archimedes. Mark the centre of the letter O.
2
Build from the center of the spiral, the circle whose radius is equal to the pitch of the helix. The pitch of the spiral of Archimedes equal to the distance travelled by the point on the surface of the circle for one complete revolution.
3
In descriptive geometry, the spiral of Archimedes relates to a radial curve. It is constructed using curves connecting the points on the circle. To get construction points, divide the circle into several equal parts with straight lines. For example, 8.
4
Number for the convenience of straight lines, dividing the circumference in the direction of rotation of the circle.
5
Divide the radius of the constructed circle to the number to which the divided circle using straight lines. With the help of a compass or ruler, divide the last in the numbering straight on the value of the marks. You only need to divide the interval between the center of the circle O and the point of intersection of a straight circle.
6
Number the marks, starting with the closest to the center of the circle. You can use numbers or letters in alphabetical order.
7
Using the compass, draw an arc of a circle center O. Arc starts from a straight line, which separated the marks and is conducted to a straight line under the number 1. Label the point where the arc is connected to the line 1 of figure 1. Similarly, construct the following arc from the marked straight line to straight at number 2. Designate a point of connection with figure 2, and then mark that point on all straight separates the circle.
8
Using the patterns, connect the center circle with the first point. Then connect the first point with the second and so connect all the marked points. You will get the first turn of the spiral of Archimedes. Try to connect the dots as evenly as possible. To get the spiral of Archimedes, higher accuracy, divide the circle into a greater number of equal parts and construct the corresponding number of arcs.