You will need
- - the range;
- a pair of compasses;
- a drafting triangle with a right angle.
Instruction
1
To determine the rectangular coordinates of the point on the plane, drop a perpendicular from this point on coordinate axes. Usually axes a and denoted as follows:• the x-axis is horizontal pointing to the right, denoted as UH;• the y-axis vertically upwards is denoted as OU.Distances from points of intersection to the origin are the coordinates of the point on the plane. The point of intersection of the perpendicular with the axis OX is called the abscissa and is denoted by x, and the point of intersection of the perpendicular with the axis OU is called the ordinate and denoted typically by y.
2
To determine rectangular coordinates of a point in space, swipe ne perpendiculars on the three axes. Usually these axes have the following location and marking:• the x-axis perpendicular to the plane of the drawing toward the observer, and is denoted as UH;• the y-axis vertically pointing upwards and designated as OU;• the axis of the applicator that con placed vertically, directed upwards and is referred to as OZ.To determine the appropriate coordinates is necessary, as in the first paragraph, to hold to each of the coordinate axes perpendicular. Then measure the distance from the point of intersection of the perpendicular with the corresponding axis to the origin.
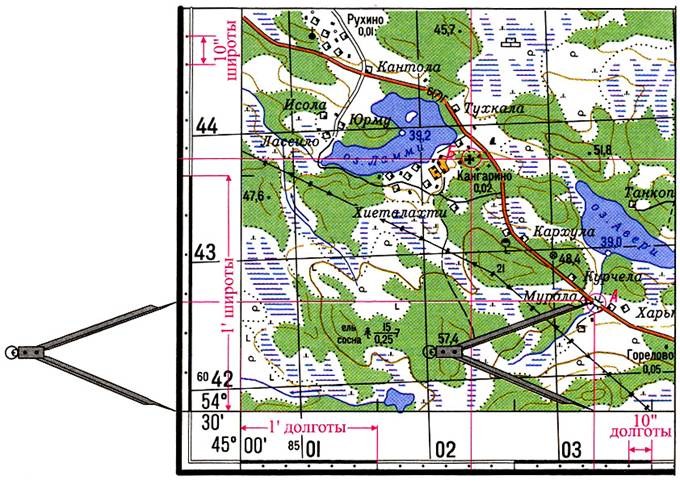
3
To determine the rectangular coordinates on the topographical map:• identify the square in which the point is located on the South side of the square, find and record the total value of the abscissa (x) in kilometers;• a pair of compasses, a ruler or koordinatorom measure the perpendicular distance from a point on the map to that coordinate line and add it to the abscissa (distance is measured in meters).The calculation of the ordinates of the points on a topographic map is similar – only instead of the South side of the square is used the Western side.