Instruction
1
The easiest way of finding the center of the circumference is to bend a sheet of paper on which it is drawn, following the gap, if the circle was folded exactly in half. The line of bend will be one of the diameters of a given circle. Then the sheet can be bent in the other direction, thereby obtaining a second diameter. Their point of intersection will be the center of the circle.This method, of course, is only suitable for cases where a circle is depicted on a sheet of paper, the paper can be bent, and have the opportunity to monitor the accuracy of the bend in the lumen.
2
Suppose that the given circle drawn on a solid material, or is it the round part, which is not possible to bend. In this case, for finding the centre you will need a ruler.Diameter, according to the definition of this word is the longest segment that can be drawn between the two points and one circle. The middle of any diameter of the circle coincides with its center.Put a ruler on a given circumference, fix the zero mark at any point on the circumference. Thus you will measure some secant, i.e. a line that connects two points of this circle. Then slowly turn the ruler, making sure you change the width of the segment. It will increase as the secant turns into the diameter, and then again will start to decrease. Noting the time of the maximum, you will find the diameter, and hence the center.
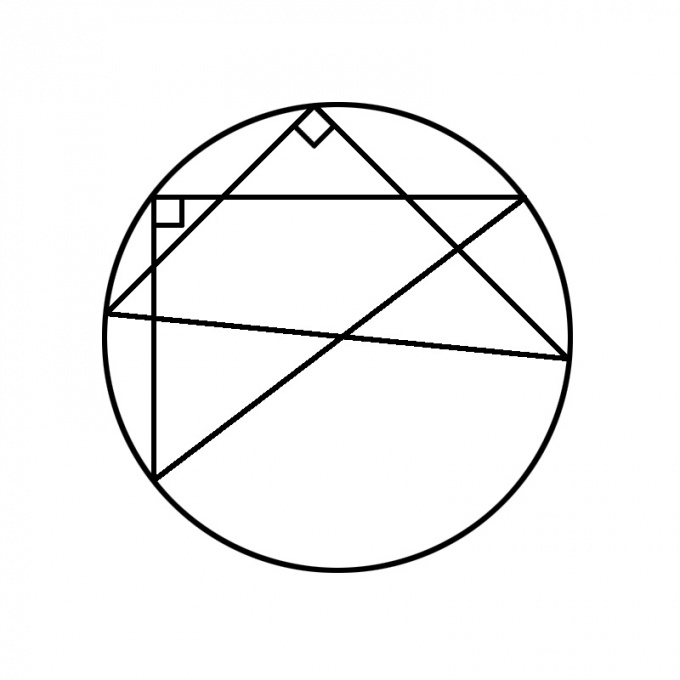
3
For any triangle the center of the described circle is the intersection of the middle perpendiculars. If the triangle is rectangular, the center of the described circle always coincides with the midpoint of the hypotenuse. Therefore, if you fit into the circle right triangle, its hypotenuse will be a diameter of this circle.As the stencil for this method, you can use any right angle — school or building the fence, or just a sheet of paper. Place the top right angle to any point on the circumference and mark where the sides of the angle intersect the circle. Are endpoints of the diameter.In the same way, find the second diameter. At the point of their intersection is the center of the circle.