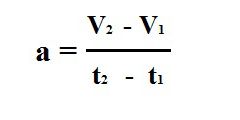How to find the speed module

Enter the coordinate system relative to which you will determine the direction and module speed. If the task is already set, the formula of dependence of speed from time to time, to introduce a system of coordinates is not necessary – it is assumed that it already is.

According to available functions of dependence of speed from time to time you can find the value of velocity at any time t. Suppose, for example, v=2t2+5t-3. If you want to find the module of the velocity at time t=1, simply substitute this value into the equation and calculate v: v=2+5-3=4.

When the task requires to find the speed at the initial moment of time, substitute in t=0. Similarly, it is possible to find the time, substituting known the speed. So, at the end of the way body has stopped, that is, its speed became zero. Then 2t2+5t-3=0. Here t=[-5±√(25+24)]/4=[-5±7]/4. It turns out that either t=-3 or t=1/2, and since time cannot be negative, we can only t=1/2.

Sometimes, the task equation is speed given in a veiled form. For example, the condition says that the body was moving uniformly accelerated with a negative acceleration of -2 m/S2, and at the initial moment the velocity of the body was 10 m/s Negative acceleration means that the body is uniformly slowed. Of these conditions you can write the equation for velocity: v=10-2t. With every second the speed will decrease by 2 m/s, until the body stops. At the end of the path speed to zero, so it is easy to find the total movement time: 10-2t=0 where t=5 seconds. After 5 seconds of motion the body will stop.

In addition to the rectilinear motion of the body, there is movement of the body around the circumference. In the General case it is curved. Here there is centripetal acceleration related to linear velocity by the formula a(c)=v2/R, where R is the radius. It is convenient to consider also the angular velocity ω, with v=ωR.